N-й степенью ненулевого числа называется произведение n множителей, каждый из которых равен заданному числу.
Число, которое умножают, называется основанием степени, число множителей является показателем степени.
Само число считают первым степенью числа и показатель степени не пишут.
Любой степень числа 1 равен единице ((.
Нулевой степень числа, отличного от нуля, равна единице: .
Степень с отрицательным показателем ненулевого числа равна числу, обратному степенью с противоположным показателем этого числа: .
Возведение в степень имеет следующие свойства:
1) Произведение степеней с одинаковым основанием равен степенью с той же основой и показателем степени, равным сумме показателей степени множителей: .
Чтобы умножить степени с одинаковой основой, нужно основу оставить без изменений, а показатели степени добавить.
2) Доля степеней с одинаковым основанием равен степенью с той же основой и показателем степени, равным разности показателей степени множителей: .
Чтобы разделить степени с одинаковой основой, нужно основу оставить без изменений, а от показателя степени делимого вычесть показатель степени делителя.
3) Степень степени равен степенью с той же основой и показателем степени, равным произведению показателей степени: .
Чтобы поднять степень в степень, нужно основу оставить без изменений, а показатели степени умножить.
4) Степень произведения множителей равен произведению степеней с тем же показателем каждого множителя: .
Чтобы поднять произведение множителей в степени, надо каждый множитель преподнести в эту степень и результаты перемножить.
5) Чтобы поднять дробь в степень, нужно поднести к этому степени и числитель, и знаменатель:.
Стандартным видом числа называется его запись в виде произведения некоторого числа, большего или равного единице, но меньшего от десяти, на степень числа десять
Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:
Из условия следует, что каждый исход равновероятен.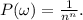
Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок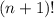 . Теперь можно считать вероятность:
. Теперь можно считать вероятность: