a) Возрастает: (-∞;0)∪(2/3;∞), убывает: (0;2/3)
б) 0 - локальный максимум, 2/3 - минимум
в) Наибольшее y=52 при x=4, наименьшее: y=4 при x=1
Объяснение:
Производная равна: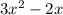 
. Отсюда x1=0, x2=2/3. Это точки экстремума.
б)
0 - максимум
2/3 - минимум
а)
На основании максимума и минимума получаем:
Функция возрастает (-∞;0)∪(2/3;∞)
Функция убывает (0;2/3)
в)
На всем промежутке от 1 до 4 функция возрастает, поэтому наименьшее значение y=4 находится при x=1, а наибольшее y=52 находится при x=4.
Нужно просто подставить 1 и 4 в функцию вместо x, чтобы вычислить y.
Решим систему уравнений
х^2+у^2=13
х-у=1.
Из второго уравнения у=х-1, подставим в 1-е уравнение
х^2+(х-1)^2=13, х^2+х^2-2х+1-13=0, 2х^2-2х-12=0,
х^2-х-6=0, D=1+4•6=25, x1=(1+5)/2=3, x2=(1-5)/2=-2-не удовл условию задачи, те х=3, у=3-1=2.
Искомое число 32.
Проверка: 3^2+2^2=13 и 32-9=23