для определения среднего дохода налогоплательщиков города налоговой инспекцией была проведена проверка 250 жителей этого города, отобранных случайным образом. оценить вероятность того, что средний годовой доход жителей города отклонится от среднего арифметического годовых доходов выбранных 250 жителей не более чем на 1000 руб., если известно, что среднее квадратичное отклонение годового дохода не превышает 2500 руб.
решение. согласно неравенству чебышева, которым можно пользоваться, поскольку все , получаем
.
теорема бернулли. если в каждом из п независимых опытов вероятность р появления события а постоянна, то при достаточно большом числе испытаний вероятность того, что модуль отклонения относительной частоты появлений а в п опытах от р будет сколь угодно малым, как угодно близка к 1:
.
замечание. из теоремы бернулли не следует, что . речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. разница заключается в следующем: при обычной сходимости, рассматриваемой в анализе, для всех п, начиная с некоторого значения, неравенство выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. этот вид сходимости называют сходимостью по вероятности.
(-6; -2)
Объяснение:
Две прямые и на плоскости называются пересекающимися, если они имеют одну общую точку. Чтобы найти координаты точки пересечения двух прямых, определенных на плоскости общими уравнениями, нужно решить систему, составленную из уравнений заданных прямых.
Составим систему уравнений:
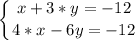
Решаем систему уравнений методом подстановки:
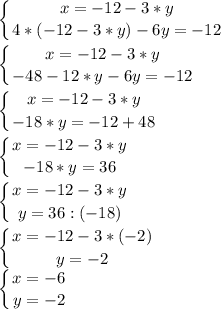
Подставляя в уравнение прямых проверим принадлежность точки (-6; -2) к прямым:
(-6)+3·(-2)= -12 и 4·(-6)-6·(-2)= -12
-6-6= -12 и -24+12= -12
-12=-12 и -12=-12, верно!
Значит, точкой пересечения прямых x+3·y= -12 и 4·x-6·y= -12 будет точка (-6; -2).
a и b - натуральные числа (Натуральные числа - это естественные положительные числа, применяемые при счете.)
{a³-b³=1603
{a-b=7 => b=a-7
Применяем формулу разности кубов
a³-b³=(a-b)(a²+ab+b²) a-b=7
7(a²+ab+b²)=1603
a²+ab+b²=229 b=a-7
a²+a(a-7)+(a-7)²=229
Применяем формулу квадрата разности (a-b)²=a²-2ab+b² для (a-7)²:
a²+a²-7a+a²-14a+49=229
3a²-21a-180=0 Все члены уравнения кратны 3, значит делим 3:
a²-7a-60=0
a₁+a₂=7
a₁*a₂=-60
a₁=12
a₂=-5 - сторонний корень, отрицательное число не соотв. условию
a=12
b=12-7
b=5
два натуральных числа, соответствующих условию: 12 и 5
Проверка:
12³-5³=1728-125=1603
12-5=7