Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
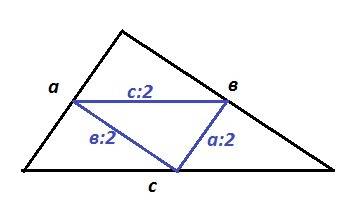
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие 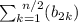 в три раза больше, чем
в три раза больше, чем 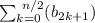
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
разделим почленно на
Замена: