сначала применим к правой части формулу приведения:
cos 2x = -cos x
cos 2x + cos x = 0
2cos²x - 1 + cos x = 0
Пусть cos x = t, причём |t| ≤ 1
2t² + t - 1 = 0
D = 1 + 8 = 9
t1 = (-1 - 3) / 4 = -1
t2 = (-1 + 3) / 4 = 1/2
cos x = -1 или cos x = 1/2
x = π + 2πn,n∈Z x = ±arccos 1/2 + 2πk,k∈Z
x = ±π/3 + 2πk,k∈Z
Данные решения могут совпадать, что разумеется нам не надо, поскольку тогда придётся писать что-то одно. В данном случае не совпадают, и это хорошо видно по числовой окружности, нанеся на неё точки π/3 и π видно, что решения никогда не наложатся одно на другое.
Поэтому, произведём отбор корней по обоим формулам.
Отберём корни из первого решения. Для этого впихнём данное решение в указанный промежуток и решим двойное неравенство относительно n:
3π/2 ≤ π + 2πn ≤ 5π/2
π/2 ≤ 2πn ≤ 3π/2
Разделим на 2п:
1/4 ≤n≤ 3/4
Видим, что никаких целых n нет на данном интервале. Значит, данное решение мы отбрасываем.
Осталось второе решение.
Также вобьём его в указанный промежуток и решим полученное двойное неравенство относительно k, но разобъём данное объединённое решение ещё на два и провернём с каждым подобную операцию:
3π/2 ≤ π/3 + 2πk ≤ 5π/2
7π/6 ≤ 2πk ≤ 13π/6
Разделим данное неравенство на 2π:
7/12 ≤ k ≤ 13/12
Замечаем, что на данном промежутке единственное целое значение k - это k = 1. Подставив его в общую формулу вместо k, получим тот самый корень, который нам требуется:
k = 1 x = π/3 + 2π = 7π/3 - это нужный отобранный корень
Теперь проверим. есть ли ещё такие корни.
Для этого впихнём в данный промежуток второй вариант решения ±π/3 + 2πk, это -π/3 + 2πk:
3π/2 ≤ -π/3 + 2πk ≤ 5π/2
11π/6 ≤ 2πk ≤ 17π/6
11/12 ≤ k ≤ 17/12
По неравенству видно, что есть опять же только единственное значение k - это 1. Подставив его в эту формулу получим наш второй корень:
k = 1 x = -π/3 + 2π = 5π/3
Таким образом, ответ пишем таким образом:
а)π + 2πn,n∈Z; ±π/3 + 2πk,k∈Z
б)7π/3; 5π/3
Под буквой б - наши отобранные корни на заданном промежутке. Задача выполнена.
x - длина одной стороны
x + 1 - длина второй стороны
Площадь равна 90 м² , значит :
x * (x + 1) = 90
x² + x - 90 = 0
D = 1² - 4 * (- 90) = 1 + 360 = 361 = 19²
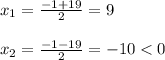
Длина одной стороны равна 9 см, а длина второй стороны 9 + 1 = 10 cм .
Детской площадке необходимо построить бордюр, значит нужно найти периметр прямоугольника :
P = 2 * (9 + 10) = 2 * 19 = 38 см
Для того, чтобы вычислить сколько упаковок материала необходимо купить, нужно периметр разделить на количество материала в одной упаковке :
38 : 20 = 1,9 - потребуется две упаковки
3Sin²x-SinxCosx=2(Sin²x+Cos²x)
Sin²x-SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим егоо на Cos²x
Tg²x-Tgx-2=0
Tgx=y
y²-y-2=0
D=9>0
y=(1+3)/2=2 или y=(1-3)/2= -1
Tgx=2⇒ x=arctg2+πn,n∈Z
Tgx= -1 ⇒x= -π/4+πk,k∈Z