Варифметической прогрессии s7=35. найдите четвертый член прогрессии.

👇

Ответ:

Михаил1946

04.03.2021

S(7)=(2a1+6d)*7/2;
(2a1+6d)*7/2=35;
(2a1+6d)*7=70;
2a1+6d=10; |:2
a1+3d=5=а4 - это и есть четвертый член прогрессии.
ответ: 5.

4,6(33 оценок)

Открыть все ответы

Ответ:

MrStepWay

04.03.2021

Для решения запишем формулу бинома Ньютона:

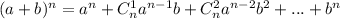
$(a+b)^n=a^n+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+...+b^n$

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение 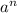a^n .

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение 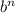b^n .

Рассмотрим многочлен 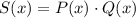$S(x)=P(x)\cdot Q(x)$ , где:

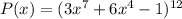
$P(x)=(3x^7+6x^4-1)^{12}$

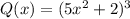
Q(x)=(5x^2+2)^3

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена 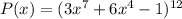$P(x)=(3x^7+6x^4-1)^{12}$ :

- степень определяется выражением 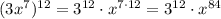$(3x^7)^{12}=3^{12}\cdot x^{7\cdot12}=3^{12}\cdot x^{84}$ , то есть степень равна 84

- свободный член равен 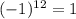$(-1)^{12}=1$

Для многочлена 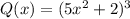Q(x)=(5x^2+2)^3 :

- степень определяется выражением 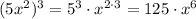$(5x^2)^3=5^3\cdot x^{2\cdot3}=125\cdot x^6$ , то есть степень равна 6

- свободный член равен 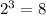2^3=8

Наконец, для многочлена 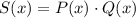$S(x)=P(x)\cdot Q(x)$ получим:

- степень определяется выражением 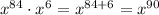$x^{84}\cdot x^6=x^{84+6}=x^{90}$ , то есть степень равна 90

- свободный член равен 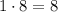$1\cdot8=8$

Сумма степени и свободного члена многочлена 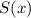S(x) :

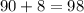
90+8=98

ответ: 98

4,5(17 оценок)

Ответ:

stefanikolaeva

04.03.2021

вначале нужно раскрыть скобки. напоминаю, что если перед скобкой стоит член, то нужно каждый член в скобках перемножить на член, стоящий перед скобкой, при чем сами скобки уберутся.

чтобы умножить скобку на скобку, нужно каждый член из первой скобки перемножить на каждый член из второй скобки.

также здесь есть формулы сокращенного умножения.

D= в²-4ас.

поехали))

1. 4х²-4х+1= 6-3х²+12

7х²-4х-17=0

D=16+476=272

х1= 4-4√17\2= 4(1-√17)\2= 2-2√17

х2= 4+4√17\2= 4(1+√17)\2= 2+2√17

ответ: 2-2√17, 2+2√17

2. х²-х-2х+2= х²-7х+6х-42

-2х-44=0