Для решения нужно написать уравнение прямой. Известно, что прямая задается уравнением у=а*х+b. Подставляя наши координаты (3;4) и (-6;-2) в уравнение прямой, получаем систему уравнений, из которой находим коэфициент а и b.
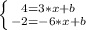. Решение относительно а дает результат 2/3, т.е. а=2/3, подставив в первое уравнение значение а, имеем b=2. Следовательно уравнение прямой у=(2/3)*х+2. Для вичисления точок пересечения с осями поочередно подставляем 0 вместо у (прямая пересекает ось ОХ), и вместо х (пресекает ось ОУ). (2/3)*х+2=0; х=-3.
(2/3)*0+2=у; у=2.
Т.е., точки пересечения с осями координат (-3;0) и (0;2).
Нельзя!
Доказательство:
Число 1 не может быть поставлено в середину ребра куба, т.к. полусумма ни одной пары оставшихся чисел не может быть равна 1. Наименьшее возможное значение такой полусуммы (2+4):2=3.
Следовательно, число 1 должно располагаться в вершине куба. Из этого вытекает, что в вершинах куба могут располагаться только нечетные числа (По условию сумма чисел, стоящих на концах ребра, должна делиться на 2 без остатка, т.е. быть четной. А сумма двух чисел, одно из которых нечетное, может быть четной только при условии, что и второе число тоже нечетное).
Из этого следует, что число 20 будет располагаться в середине какого-либо ребра куба. Очевидно, что число 20 не может быть полусуммой каких-либо двух чисел, каждое из которых меньше 20.
Вывод: расположить числа указанным в задаче невозможно.
заменяем t=2x-7
получаем t²-11t+30=0
D=11²-4*30=121-120=1
t1=(11-1)/2=5 2x1-7=5 x1=6
t2=(11+1)/2=6 2x2-7=6 x2=6,5
ответ: 6 и 6,6
(6x+1)²+2(6x+1)-24=0
t=6x+1
t²+2t-24=0
D=2²+4*24=4+96=100
√D=10
t1=(-2-10)/2=-6. 6x1+1=-6. x1=-7/6 =-1 1/6
t2=(-2+10)/2=4. 6x2+1=4. x2=0,5
ответ: -1 1/6 и 0,5