Найдём производную функции
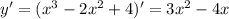
Теперь найдём критические точки(y'=0):
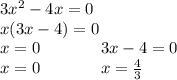
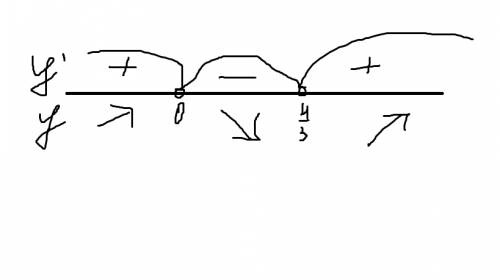
Начертим прямую, нанесём точки на интервал. Там где производная положительная функци возрастает, отрицательная убывает. Там где функция сначало возрастала(убывала), а после в какой-то точке начало убывать(возрастать), то это точка экстрэмума.
Вложение.
Промежутки возрастания, убывания(промежутки монотонности):
(-бесконечности;0] - возрастает
(0;4/3] - убывает
(4/3;+бесконечности) - возрастает.
Экстэмумы функции: 0 - точка максимума.
4/3 - точка минимума.
Рисунок вложение.
Чтобы найти наибольшее и наименьшее значение на отрезке нужно найти значения на функции на концах отрезков, и на точках которые входят в этот промежуток. У нас это точки: -1;4;0;4/3
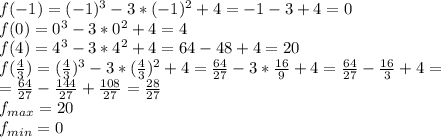
уравнение касательной:
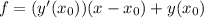
Найдём y(x0):
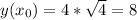
Найдём производную.
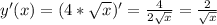
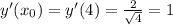
Подставим в уравнение касательной.
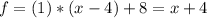

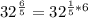
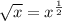
![\sqrt[3]{x} =x^{\frac{1}{3}}](/tpl/images/0503/0859/f093d.png)
![32^{ \frac{1}{5}} =\sqrt[5]{32}](/tpl/images/0503/0859/6c7d6.png)
![\sqrt[5]{32}=\sqrt[5]{2^{5}}](/tpl/images/0503/0859/ad486.png)
![\sqrt[5]{2^{5}}=2^{\frac{5}{5}}=2](/tpl/images/0503/0859/67bfa.png)
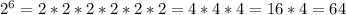
если a=5, b=2, c=3, то 5·(5)²·2·(3)³=5³·2·27=125·2·27=6750.
ответ: 6750.