Коэффициент подобия по определению считается по линейным размерам .
Для периметра (сумме линейных размеров) он равен k, для площадей k^2,
для объемов k^3.Тогда периметр равен 12*4=48 см, площадь равна 9*4^2=144 кв. см
Как-то так
Объяснение:
<!--c-->
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
P(ABC)P(RTG)=k20P(RTG)=19P(RTG)=9⋅20=180(см)
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
S(ABC)S(RTG)=k26S(RTG)=(19)26S(RTG)=181S(RTG)=6⋅81=486(см2)
31) y = - x² + 2x + 10
Графиком является парабола, ветви которой направлены вниз, так как a = - 1 < 0 . Найдём абсциссу вершины параболы :
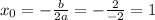
Найдём ординату вершины параболы :
y₀ = - 1² + 2 * 1 + 10 = - 1 + 12 = 11
ответ : область значений функции y ≤ 11
32) y = x² + 10x + 8
Графиком является парабола, ветви которой направлены вверх, так как a = 1 > 0 .
Найдём абсциссу вершины параболы :
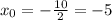
Найдём ординату вершины параболы :
y₀ =(-5)² + 10 * (- 5) + 8 = 25 - 50 + 8 = - 17
ответ : область значений функции y ≥ - 17
24x-45y+48z