ответ:Чтобы разложить данные выражения на множители, надо преобразовать их в произведения, используя при этом формулы сокращенного умножения;
1) аb - 3 b + b^2 - 3 a, применим группировки;
(a b + b2) - (3 b + 3 a), из каждой скобки вынесем общий множитель;
b * (a + b) - 3 * ( b + a), теперь вынесем общий множитель выражения;
(a + b) * (b - 3).
2) 11 х - х у + 11 y - х^2, аналогично решению предыдущего примера, разложим на множители следующие выражения;
(11 x + 11 y) - (x^2 + x y) = 11 * (x + y) - x * (x + y) = (x + y) * (11 - x)
3) k n - m n - n^2 + m
Объяснение:
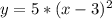
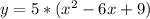
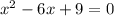
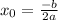
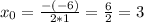
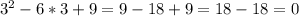
an=a1+d(n-1)=11,2-0,4(n-1)=11,2-0,4n+0,4=11,6-0,4n
решим неравенство
11,6-0,4n>0
0,4n<11,6
n<29
количество положительных членов меньше 29, значит: n=28
найдём an=a28
a28=11,6-0,4*28=11,6-11,2=0,4
S28=(a1+a28)*n/2=(11,2+0,4)*28/2=11,6*14=162,4
ответ: 162,4