Чокан Валиханов был чингизидом — правнуком Абылай-хана. Дед Чокана Вали-хан — один из 30 сыновей Абылай-хана. Чокан Валиханов родился в орде-зимовке Кунтимес Аманкарагайского внешнего округа (ныне аул Кунтимес в Сарыкольском районе Костанайской области). Кунтимес была постоянной зимовкой 1834—1853 гг. его отца Чингиса Валиханова[10], старшего султана Аманкарагайского (с 1845 г. Кушмурунского) округа Омской области. При рождении мальчику было дано мусульманское имя Мухаммед-Канафия. Позже придуманное его прозвище Чокан закрепилось как официальное имя. В детстве (1842—1847 гг.) мальчик учился в казахской школе, открытой в орде Кунтимес, где он получил начальные знания казахского, кыпшак-чагатайского, арабского и персидского языков.
Объяснение:
ДАНО:Y(x) = x^3 -12*x² +36*x +()
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
Разложим многочлен на множители. Y=(x-0)*(x-6)*(x-6)
Нули функции: Х₁ =0, Х₂ =6, Х₃ =6
3. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;0]. Положительная -Y(x)>0 X∈[0;+∞)
4. Пересечение с осью OY. Y(0) = 0.
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
6. Первая производная. Y'(x) = 3*x² -24*x + 36 = 0
Корни Y'(x)=0. Х4=2 Х5=6
Положительная парабола - отрицательная между корнями
7. Локальные экстремумы.
Максимум Ymax(X4=2) =32. Минимум Ymin(X5=6) =0
8. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;2;]U[6;+∞) , убывает - Х∈[2;6]
9. Вторая производная - Y"(x) = 6* x -24 = 0
Корень производной - точка перегиба Х₆=4
10. Выпуклая “горка» Х∈(-∞; Х₆=4]
Вогнутая – «ложка» Х∈[Х₆=4; +∞).
11. График в приложении.
Дополнительно: шаблон для описания графика.
Объяснение:
1. а)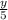 ∈{-2,-1} ⇒ y∈{-10,-5} (условие выполняется)
∈{-2,-1} ⇒ y∈{-10,-5} (условие выполняется)
б)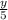 ∈{0}, тогда 0<1, но 0<3 ⇒ противоречие
∈{0}, тогда 0<1, но 0<3 ⇒ противоречие
в)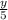 ∈{-5, -1}, y∈{-10,-5}
∈{-5, -1}, y∈{-10,-5}
г)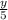 ∈{15}, y∈{75}, но y<5 ⇒ противоречие
∈{15}, y∈{75}, но y<5 ⇒ противоречие
2. a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}
a) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}
б) a∈{5,6,7}, b∈{9,10,11,}, a+b∈{14,15,16}
в) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12} a+b∈{14,15,16,17,18}
3. A) a>0
б) a < 0
в) a-8 (всегда) < a + 8 ⇒ противоречие
г) при возведение в квадрат любого числа получится положительное ⇒ когда мы поменяем его на отрицательный после возведения, полученное значение будет < 0. Но при возведение 0^2 = 0 ⇒ a=3 единственное решение.
4. p ∈ {10, 11, 12, 13}
а) если p ∈ {10, 11, 12, 13}(по условию), то выполняется только одно из условий ⇒ противоречие
б) p ∈ {10, 11, 12, 13}
в) значение всех трех дробей должно быть отрицательным чтобы соблюдалось условие, но так как >0 приходим у противоречию
>0 приходим у противоречию
г) аналогично в
5. а), в)
6. x - а), в), г)
y - б)