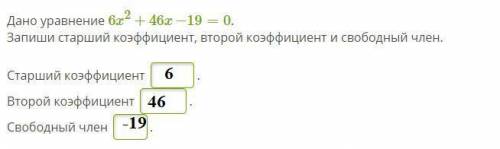
№1 (ответ на фото)
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причём, а≠0. Коэффициенты а, b, с, различают по названиям: а - первый или старший коэффициент; b - второй или коэффициент при х; с - свободный член, свободен от переменной х
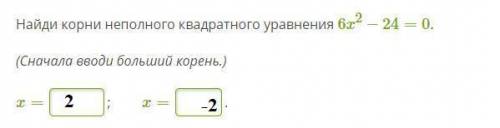
№2 ( ответ на фото)
Приведенное квадратное уравнение – уравнение вида , первый коэффициент которого равен единице
№3.
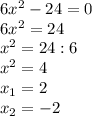
ответ: ±2
№4.
8x²+6x+9=0
a=8 b=6 c=9
D=b^2-4ac=6^2-4*8*9=36-288=-252
№5
x²+14x-8=0
D=14²-4*1*(-8)=196+32=228
√D=√228=2√57
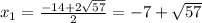
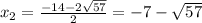
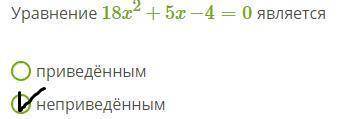


Сначала узнаем сколько всего чисел, кратных 102 и не превышающих 10000. Для этого достаточно вычислить неполное частное при делении 10000 на 102, это 98.
Перед нами последовательность чисел, каждое из которых делится на 102: {1·102; 2·102; 3·102; ... ; 98·102}. Узнаем, какие из этих чисел кратны 14 и 15.
Заметим, что 102 = 2·3·17, а 14 = 2·7. Числа в нашей последовательности имеют вид 102n. Тогда число такого вида будет делиться на 7, если n кратно 7. Количество таких чисел можно также найти при делении 98 на 7, это 14. Аналогично и для 15 = 3·5 можно получить, что чисел, кратных 15, в нашей последовательности [98/5] = 19 ([x] - целая часть числа x).
Итак, у нас есть 98 чисел кратных 102, из них 14 чисел кратны 14, а 19 чисел кратны 15. Тогда количество чисел, удовлетворяющих условию: 98 - 14 - 19 = 65.
Хотел бы я так сказать, однако всего их не 65 :)
Дело в том, что в нашей последовательности есть числа, которые делятся и на 14, и на 15, а мы это не учли (в нашем ответе числа такого рода вычитались по 2 раза). Это легко исправить, если узнать, сколько чисел делятся и на 14, и на 15.
Число делится и на 14, и на 15 тогда и только тогда, когда оно делится на НОК(14, 15) = 210.
Заметим, что 210 = 2×3×5×7, а 102 = 2·3·17 (как уже выяснялось ранее). Значит, числа вида 120n делятся на 210, если n кратно 35. Количество таких чисел: [98/35] = 2.
Тогда у нас 65+2 = 67 чисел, удовлетворяющих условию. Можно писать ответ.
ответ: 67.