1) 
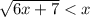
Составим систему неравенств, учитывая каждое ограничение, накладывающееся на аргумент:
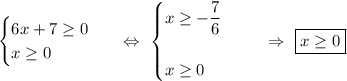
Теперь продолжаем решать наше неравенство.
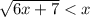
Возведём обе части неравенства в квадрат.
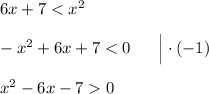
Получаем квадратное неравенство. Чтобы найти нули, приравняем левую часть к 0 и найдём корни квадратного уравнения.
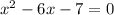
По теореме Виета:
Возвращаемся к неравенству:
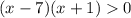
Решим его методом интервалов.
Нули: 7; -1.
+ - +
---------------------о------------------------------о-----------------------> х
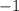
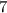
Получаем, что решением квадратного неравенства являются промежутки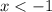 
и 
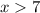. Но не забываем про ограничение 
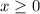, которое мы вычислили выше.
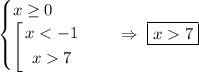
ответ: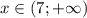 
.
2) 
Это задание можно решить методом интервалов. Нужно найти нули. С левым множителем понятно, он обращается в 0 при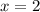 
. Приравняем правый множитель к нулю, чтобы найти его корни.
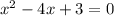
По теореме Виета:
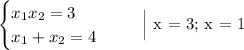
Применяем метод интервалов для нашего неравенства.
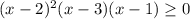
Нули: 1; 2; 3.
+ - - +
---------------
-------------------------------------------------------------> x
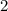
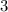
Так как знак неравенства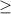 
, то нам нужны те промежутки где стоит знак +. Таких два: 
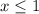и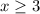 
, но и это ещё не всё. Есть ещё точка 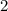, и она тоже является решением, поскольку при ней выражение обращается в 0.
ответ: ![(-\infty; 1] \cup [3; +\infty) \cup \left \{2\right \}](/tpl/images/1583/3218/3e3e3.png)
.
1) Если требуется найти ВСЕ ОБЩИЕ РЕШЕНИЯ нескольких уравнений, то говорят, что надо решить систему уравнений.
2) Решением системы уравнений с двумя переменными называют ПАРУ ЗНАЧЕНИЙ ПЕРЕМЕННЫХ,ОБРАЩАЮЩУЮ КАЖДОЕ УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО.
3) Решить систему уравнений - это значит НАЙТИ ВСЕ РЕШЕНИЯ ИЛИ ДОКАЗАТЬ,ЧТО РЕШЕНИЙ НЕТ.
4) Суть графического метода решения системы уравнений состоит в следующем:
а) построить на одной координатор плоскости ГРАФИКИ УРАВНЕНИЯ, ВХОДЯЩИЕ В СИСТЕМУ.
б) найти КООРДИНАТЫ ВСЕХ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПОСТРОЕННЫХ ГРАФИКОВ
в) ПОЛУЧЕННЫЕ ПАРЫ ЧИСЕЛ и будут искомыми решениями
5) Если одно из уравнений системы не имеет решений, то вся система РЕШЕНИЙ НЕ ИМЕЕТ.
6) Если каждое уравнение системы линейных уравнений имеет решение и графиком одного из уравнений является вся плоскость, то система имеет БЕСКОНЕЧНО МНОГО РЕШЕНИЙ.
7) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ НА ПЛОСКОСТИ:
а) если прямые ПЕРЕСЕКАЮТСЯ, то система имеет единственное решение
б) если прямые СОВПАДАЮТ, то система имеет бесконечно много решений
в) если прямые ПАРАЛЛЕЛЬНЫ, то система решений не имеет.
Объяснение:
Квадрат выражения в скобках - число неотрицательное при любых значениях х, а значит вся сумма - число положительное.