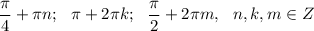Решите тригонометрические уравнения. хотя бы одно! cos(7x)-cos(x)-sin(4x)=0 sin^2(x)+6cos^2(x)+7sin(x)cos(x)=0 4sin^2(x)+5sin(x)cos(x)-cos^2(x)=2 sin(2x)+корень из 2* sin(x-п/4)=1
{a1+ a6=11 a2+a4=10 Выразим а2, а4 , а6 через первый член арифметической прогрессии и разность прогрессии (d) a2=a1+d a4=a1+3d a6=a1+5d и подставим в систему: {a1+a1+5d=11 a1+d+a1+3d=10 {2a1+5d=11 2a1+4d=10 Решим систему методом сложения. Умножим первое уравнение на (-1) и сложим со вторым: {-2a1-5d=-11 + 2a1+4d=10 -d=-1 d=1 2a1+4=10 a1=3 (подставили найденное значение d во второе уравнение системы и нашли первый член прогрессии.) По формуле суммы n-первых членов прогрессии найдём сумму первых шести членов этой прогрессии: S6=(2·3+5 )\2·6=33 (Sn=(2a1+d(n-1))\2·n) ответ:33
ОДЗ : х² - 5х - 23 ≥ 0 2х² - 10х - 32 ≥ 0 Решение системы двух неравенств не так просто, поэтому при нахождении корней достаточно сделать проверку. Подставить корни в систему неравенств или подставить корни в уравнение
Так как 2х²-10х-32=2(х²-5х-16) то применяем метод замены переменной
х²-5х-23=t ⇒ x²-5x=t+23 x²-5x-16=t+23-16=t+7
Уравнение примет вид √t + √2·(t+7)=5
или
√2·(t+7) = 5 - √t
Возводим обе части уравнения в квадрат При этом правая часть должна быть положительной или равной 0 ( (5 - √t)≥0 ⇒√ t ≤ 5 ⇒ t ≤ 25)
2·( t + 7) = 25 - 10 √t + t
или
10·√t = 25 + t - 2t - 14
10·√t = 11 - t
Еще раз возводим в квадрат, при условии, что 11 - t ≥ 0 t ≤ 11 Получаем уравнение
100 t = 121 - 22 t + t², при этом t ≤ 11
t² - 122 t + 121 = 0
D=122²-4·121=14884 - 484 = 14400=120
t₁=(122-120)/2= 1 или t₂= (122+120)/2 = 121 не удовлетворяет условию ( t ≤ 11)
ответ: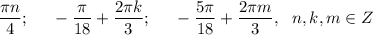
---------------------------------------------------------------------------------------
ответ: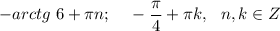
----------------------------------------------------------------------------------------
ответ: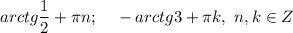
-----------------------------------------------------------------------------------------
ответ: