Объяснение:
Задано число:
52*2*
Заметим, что
36 = 4*9, то есть число должно делиться и на 4, и на 9.
1)
Признак делимости на 4:
Число делится на 4, если его запись оканчивается двумя цифрами, образующими число, которое делится на 4 или его запись оканчивается двумя нулями.
Поскольку предпоследняя цифра не равна нулю, то остаются кандидаты:
20; 24 и 28.
2)
Признак делимости на 9:
Число делится на 9, если сумма цифр целого числа делится на 9.
Заметим, что сумма трех цифр нашего числа уже делится на 9:
5+2+2=9 - делится на девять.
Рассмотрим три последние цифры.
*2*
Заметим, что последняя цифра - четная (число должно делиться на 4).
Возможные комбинации:
020 (0+0=0)
128 (1+8=9)
326 (число 26 не делится на 4)
524 (5+4=9)
722 (число 22 не делится на 4)
920 (9+0=9)
Осталось 4 числа:
52020
52128
52524
52920
Перенесем все влево и вынесем за скобки  :
:
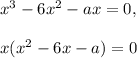
Из этого следует, что уравнение всегда имеет хотя бы одно решение -  . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения  и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении  корнем уравнения
корнем уравнения  будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 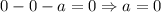 . При
. При  имеем:
имеем:

Делаем вывод, что при  уравнение имеет два корня:
уравнение имеет два корня: 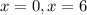 .
.
2) при 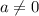 уравнение
уравнение  не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 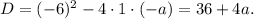
Здесь рассматриваем 3 случая:
2.1. Если  , то уравнение
, то уравнение  решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если 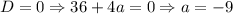 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 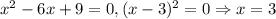 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если 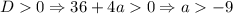 , то уравнение
, то уравнение  имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит  , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при  корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При  уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 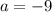 и
и  уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 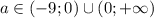 уравнение имеет три различных корня.
уравнение имеет три различных корня.