Объяснение:
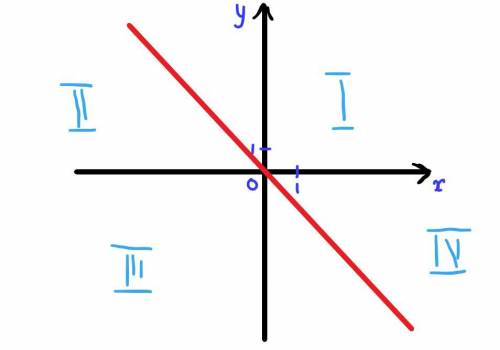
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна 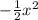
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.
Объяснение:
Разберем подстановки на примере.
x + 5y = 7
3x − 2y = 4
Выразим из первого уравнения «x + 5y = 7» неизвестное «x».
Перенесём в первом уравнении «x + 5 y = 7» всё что содержит «x» в левую часть, а остальное в правую часть по правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.
x = 7 − 5y
3x − 2y = 4
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
x = 7 − 5y
3(7 − 5y) − 2y = 4
Подставив вместо «x» выражение «(7 − 5y)» во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным «y». Решим его по правилам решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение «3(7 − 5y) − 2y = 4» отдельно. Вынесем его решение отдельно с обозначения звездочка (*).
x = 7 − 5y
3(7 − 5y) − 2y = 4 (*)
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1». Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение. Таким образом можно найти «x». Запишем в ответ оба полученных значения.
x = 7 − 5y
y = 1
x = 7 − 5 · 1
y = 1
x = 2
y = 1
ответ: x = 2; y = 1
12x-8x+3x=-4-3
7x=-7
x=-7 : 7
x=-1