Ученик - за 15 часов, мастер - за 5 часов.
Объяснение:
Пусть х часов нужно ученику чтобы выполнить работу, тогдамастеру нужно x-10 часов. Примем работу за единицу, тогда за час ученик выполняет 1/х работы, мастер - 1/(х-10). Из условия следует что за час работы вместе они выполнят 1/3.75 работы. Составим и решим уравнение:
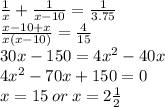
Если ученик выполняет работу за 2.5 часа, то мастер выполняет её за -7.5 часов, но т.к. время - положительная величина, то ученик не мог выполнить работу за 2.5 часа => он выполнил её за 15 часов, а местер за 5 часов
x^4 - 2x^2 + 1 = ( x^2 - 1 )^2 = ( x^2 - 1 )( x^2 + 1 )( x^2 - 1 )( x^2 + 1 ) =
= ( x - 1 )( x + 1 )( x - 1 )( x + 1 )( x^2 + 1 )^2
3) ( ( x - 1)( x - 1 )( x + 1 )) / ( ( x - 1 )( x + 1 )( x - 1 )( x + 1 )( x^2 + 1 )^2 ) =
= ( x + 1 ) / ( x^2 + 1 )^2