Somebody says something toy you which is not what you expected. use you own ideas to complete your answers. a: sarah gets on fine with paul. b: does she? last week you said each other.

👇

Увидеть ответ

Ответ:

Lika4072004

01.05.2021

Это же не .. completely

4,7(40 оценок)

Открыть все ответы

Ответ:

Qwerty23459484

01.05.2021

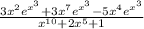
$\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1}$

Объяснение:

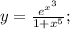
$y=\frac{e^{x^{3}}}{1+x^{5}};$

Производная дроби находится по следующей формуле:

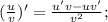
$(\frac{u}{v})'=\frac{u'v-uv'}{v^{2}};$

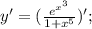
$y'=(\frac{e^{x^{3}}}{1+x^{5}})';$

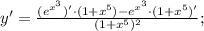
$y'=\frac{(e^{x^{3}})' \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};$

Функция

$e^{x^{3}}$

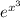
является сложной функцией. Производная сложной функции находится по следующей формуле:

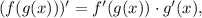
$(f(g(x)))'=f'(g(x)) \cdot g'(x),$

отсюда получаем

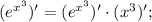
$(e^{x^{3}})'=(e^{x^{3}})' \cdot (x^{3})';$

Если ввести замену

$t=x^{3},$

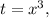
то выражение

$e^{x^{3}}$

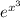
преобразуется как

$e^{t}.$

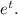
Производная последнего выражения является табличным значением:

$(e^{t})'=e^{t};$

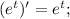
Возвращаясь к замене, получаем:

$e^{x^{3}}.$

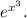
Производная второго множителя находится по следующей формуле:

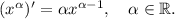
$(x^{\alpha})'=\alpha x^{\alpha-1}, \quad \alpha \in \mathbb {R}.$

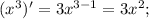
$(x^{3})'=3x^{3-1}=3x^{2};$

Подставим полученные значения в произведение:

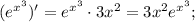
$(e^{x^{3}})'=e^{x^{3}} \cdot 3x^{2}=3x^{2}e^{x^{3}};$

Подставим значение этой производной в дробь:

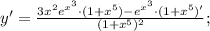
$y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot (1+x^{5})'}{(1+x^{5})^{2}};$

Производная суммы равна сумме производных:

(u+v)'=u'+v';

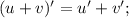
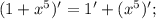
$(1+x^{5})'=1'+(x^{5})';$

1 — константа. Производная константы равна нулю.

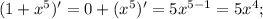
$(1+x^{5})'=0+(x^{5})'=5x^{5-1}=5x^{4};$

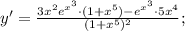
$y'=\frac{3x^{2}e^{x^{3}} \cdot (1+x^{5})-e^{x^{3}} \cdot 5x^{4}}{(1+x^{5})^{2}};$

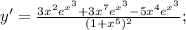
$y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{(1+x^{5})^{2}};$

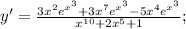
$y'=\frac{3x^{2}e^{x^{3}}+3x^{7}e^{x^{3}}-5x^{4}e^{x^{3}}}{x^{10}+2x^{5}+1};$

4,7(55 оценок)

Ответ:

kceniakey

01.05.2021

Промежутки знакопостоянства — такие промежутки на области определения, в которых значения функции сохраняют свой знак.

1. Нули функции- это значения аргумента при которых функция равна нулю. Для нахождения их надо функцию приравнять к нулю и решить это уравнение.

2. Это числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной), называются промежутками знакопостоянства функции.

3. Возрастающая функция - это функция, при которой большему значению аргумента (х) соответствует большее значение функции (y).

4. Убывающая функция - это функция, при которой большему значению аргумента (х) соответствует меньшее значение функции (у).

5. Это функция, при которой большему значению аргумента (х) соответствует большее значение функции (y)

6. Функция, значения которой по мере увеличения аргумента уменьшаются

4,8(10 оценок)

Это интересно:

Семейная-жизнь

30.12.2022

Как справиться с желтухой новорожденного?...

Стиль-и-уход-за-собой

30.01.2020

Как выбрать правильный продукт для женской гигиены...