найдем одз. под корнем может находиться только неотрицательное значение, значит 5-х> =0, откуда х< =5. корень может принимать только неотрицательные значения, значит 5-х^2> =0, откуда х^2< =5, откуда |х|< =√5, откуда -√5< =х< =√5.
теперь решение:
вoзведем в квадрат:
(5-x^2)^2=5-x
25-10x^2+x^4=5-x
x^4-10x^2+x+20=0
(x^2-x-4)(x^2+x-5)=0
1) x^2-x-4=0
d=17
x(1)=(1+√17)/2> (1+√16)/2=(1+4)/2=5/2=√5*√5/2> √5*√4/2=√5. значит этот корень не подходит.
x(2)=(1-√17)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
2) x^2+x-5=0
d=21
x(1)=(-1+√21)/2 подставляя в изначальное уравнение, проверяем, что этот корень подходит.
x(2)=(-1-√21)/2< (-1-√16)/2=-5/2=-√5*√5/2< -√5*√4/2=-√5. значит этот корень не подходит.
ответ: х(1)=(1-√17)/2, х(2)=(-1+√21)/2.
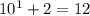кратне 3
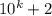кратне 3
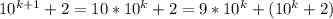кратне 3, там як перший доданок кратний 3 (перший множник добутку 9 кратний 3), другий кратний у силу припущення індукції. 
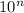=10000....0 (одна одиниця, n нулів, причому нуль остання цифра),то
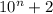=10000...0002(одна одиниця, n-1 нуль, одна 2) 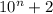дасть залишок такий же як дасть залишок від ділення суми залишків чисел 1 + 2 =3 , залишок 0 (так як 3 кратне 3), а значить задане число кратне 3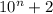=3*3333...34 (n-1 трійка і 1 четвірка)
Пусть хкм/ч -скорость лодки в стоячей воде, тогда время затраченное на прохождения расстояния по течению будет равно 80/(х+4)ч, а против течения
80/(х-4)ч. Тогда, зная что туда и обратно лодка затратила (8+1/3)ч составим уравнение:
80/(х+4)+80/(х-4)=8+1/3
(80(x-4)+80(x+4))/(x+4)(x-4)=25/3 |умножим обе части уравнения на 3(х+4)(x-4) неравное нулю
240(x-4+x+4)-25(x+4)(x-4)=0
240*2x-25(x^2-16)=0
480x-25x^2+400=0 |разделим обе части уравнения на -5
5x^2-96x-80=0
D= 9216+1600=10816=104^2
x1=(96+104)/10=200/10=20
x2=(96-104)/10=-8/10=0-этот корень нам не подходит, т.к. скорость не может быть отрицательной=> x=20, т.е. скорость в лодки в стоячей воде 20км/ч
ответ: скорость в лодки в стоячей воде 20км/ч