1.
– 6x – 23 = – 9x – 5
– 6x + 9x = – 5 + 23
3x = 18
x = 6
2.
8x – 6 = 5x + 3
8x – 5x = 3 + 6
3x = 9
x = 3
3.
6x + 7 = 20x – 5 – 16
6x – 20x = – 16 – 5 – 7
-14x = -28
x = 2
4.
15x – 12x – 20 = 14x + 35
15x – 12x – 14x = 35 + 20
-11x = 55
x = -5
5.
15x – 40 – 6 + 15x = 4x – 20
15x + 15x – 4x = – 20 + 6 + 40
26x = 26
x = 1
6.
2(x-23)+3(15-x)=-x+1
2x – 46 + 45 – 3x = – x + 1
2x – 3x + x = 1 – 45 + 46
0x = 2
Какой бы x мы ни взяли, это уравнение не превратится в верное равенство. Значит, это уравнение решений не имеет!
Выделим полный квадрат:
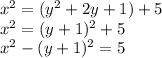
Раскладываем левую часть по формуле разности квадратов:
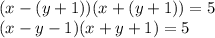
5 можно разложить в произведение двух сомножителей следующими
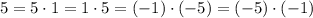
Это позволяет заменить рассмотрение уравнение на совокупность из четырёх систем:
1) x - y - 1 = 5, x + y + 1 = 1
Складываем и вычитаем уравнения:
2x = 5 + 1, 2y + 2 = 1 - 5
x = 3, y = -3
2) x - y - 1 = 1, x + y + 1 = 5
2x = 1 + 5, 2y + 2 = 5 - 1
x = 3, y = 1
3) x - y - 1 = -1, x + y + 1 = -5
2x = -1 - 5, 2y + 2 = -5 + 1
x = -3, y = -3
4) x - y - 1 = -5, x + y + 1 = -1
2x = -5 - 1, 2y + 2 = -1 + 5
x = -3, y = 1
Этот же ответ можно было получить из первого решения и того, что если (x, y) – решение, то и (-x, y) и (x, -2 - x) – решение.
ответ. (3, -3), (3, 1), (-3, -3), (-3, 1)
Применяем формулу классической вероятности
р=m/n
Находим m в каждом событии
а) А-сумма очков на верхних гранях нечетная и на одном из кубиков выпало 4 очка
Cобытию А благоприятствуют два исхода испытания.
На одном кубике 4, на другом 1
На одном кубике 1, на другом 4
m=2
р(А)=2/36=1/18
б)Б-сумма очков, выпавших на верхних гранях, не больше 6
Cобытию Б благоприятствуют десять исходов испытания.
На одном кубике 1, на другом 4
На одном кубике 1, на другом 3
На одном кубике 1, на другом 2
На одном кубике 1, на другом 1
На одном кубике 2, на другом 1
На одном кубике 2, на другом кубике 2
На одном кубике 2, на другом кубике 3
На одном кубике 3, на другом 2
На одном кубике 3, на другом 1
На одном кубике 4, на другом 1
m=10
р(Б)=10/36=5/18
в)В-сумма очков, выпавших на верхних гранях, не меньше 5 и не больше 8
Cобытию В благоприятствуют исхода испытания.
На одном кубике 1, на другом 4
На одном кубике 1, на другом 5
На одном кубике 1, на другом 6
На одном кубике 2, на другом 3
На одном кубике 2, на другом 4
На одном кубике 2, на другом 5
На одном кубике 2, на другом 6
На одном кубике 3, на другом 2
На одном кубике 3, на другом 3
На одном кубике 3, на другом 4
На одном 3, на другом 5
На одном 4, на другом 1
На одном 4, на другом 2
На одном 4, на другом 3
на одном 4, на другом 4
На одном 5, на другом 1
На одном 5, на другом 2
На одном 5, на другом 3
На одном 6, на другом 1
На одном 6, на другом 2
m=20
р(В)=20/36=5/9
г)Г-сумма очков, выпавших на верхних гранях равна пяти, а модуль разности равен очков равен 3
5=1+4, |1-4|=3
5=4+1, |4-1|=3
m=2
р(Г)=2/36=1/18
д)сумма очков, выпавших на верхних гранях равна семи, а их произведение равно 10
m=2
На одном 2, на другом 5
На одном 5, на другом 2
р(Д)=2/36=1/18