В решении.
Объяснение:
1) Решить уравнения:
а)х²-3х-40=0
х₁,₂=(3±√9+160)/2
х₁,₂=(3±√169)/2
х₁,₂=(3±13)/2
х₁= -10/2
х₁= -5
х₂=16/2
х₂=8
б)(х-7)²=2х²+11х+23
х²-14х+49=2х²+11х+23
х²-14х+49-2х²-11х-23=0
-х²-25х+26=0/-1
х²+25х-26=0
х₁,₂=(-25±√625+104)/2
х₁,₂=(-25±√729)/2
х₁,₂=(-25±27)/2
х₁= -52/2
х₁= -26
х₂=2/2
х₂=1
в)(х-8)(12-3х)=0
х-8=0
х₁=8
12-3х=0
-3х= -12
х₂=4
2)Упростить:
а)(b+4)²-2b(5b+4)=
=b²+8b+16-10b²-8b=
= -9b²+16=
= -(9b²-16)=
= -(3b-4)(3b+4);
б)(b-8)²-2b(7b-8)=
=b²-16b+64-14b²+16b=
= -13b+64;
в)12а-2(а+3)²=
=12а-2(а²+6а+9)=
=12а-2а²-12а-18=
= -2а²-18=
= -2(а²+9).
см. рисунок
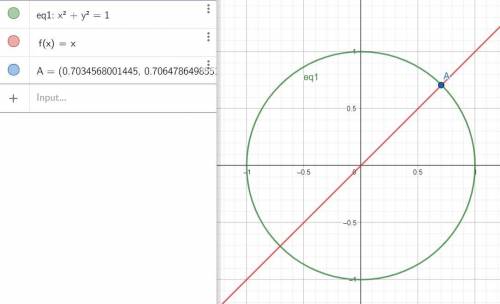
1) А
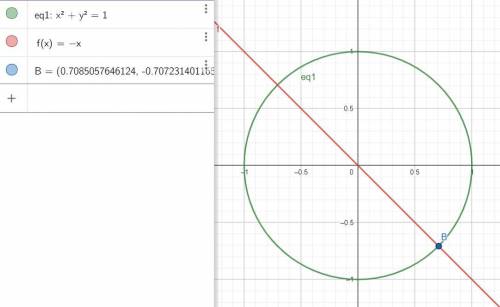
2) В
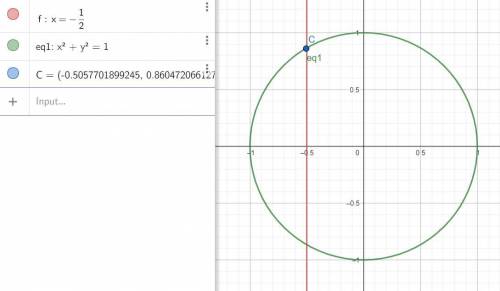
3) С
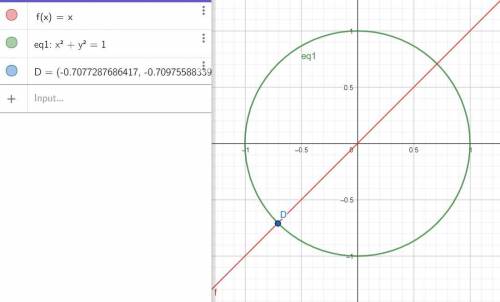
4) D
Объяснение:
а) 2пи - полный оборот, поэтому все точки будут слиты в одну. 6 пи, 8 пи кратны 2 пи поэтому там то же самое. вывод: достаточно построить 1 точку в каждом случае
б) пи на четыре = 45 градусов. табличное значение.
в) пи на три = 60 градусов. табличное значение
г) при единичном круге х = косинус угла поворота у = синус угла поворота
д) реально строить хорошо - прочертить круг и пересекать его лучом соответствующего угла отклонения. Для 1) и 2) и 4)
Для 3) 2 пи на три = 120 градусов, т.е. 90 + 30, у єтих точек абсциса (х) будет = 1/2 по табличному значению синуса - посему - линия по этой абсцисе - и точка пересечения с кругом - искомая.
потянет на лучший ответ?
√3≈1,73
поэтому 1+√2+√3≈4,14
Отсюда получаем, что целочисленные решения неравенства |x|≥1+√2+√3 это числа +-5, +-6, +-7 и т. д.
теперь решим неравенство х²-7х+6 ≤0
D=7²-4*6=49-24=25
√D=5
x₁=(7-5)/2=1
x₂=(7+5)/2=6
х²-7х+6 =(x-6)(x-1)≤0
целочистленными решениями неравнства будут числа 1,2,3,4,5 и 6. Всего 6 чисел. Только числа два числа из них - 5 и 6 -являются также решениями неравенства |x|≥1+√2+√3
Соответвенно искомая вероятность 2/6=1/3