Построим график функции у = 8 + 2x - x²
Для этого преобразуем её к виду
у = -(х² - 2х + 1) + 9
у = -(х - 1)² + 9
Видим, что парабола у = -х² сдвинута по оси абсцисс на 1 вправо и на 9 вверх. То есть её вершина находится в точке с координатами (1; 9).
Найдём координаты точек пересечения параболы с осью ординат.
При х = 0 у = 8
И координаты точек пересечения параболы с осью абсцисс
у = 0
- х² + 2х + 8 = 0
D = 2² - 4 · (-1) · 8 = 36
√D = 6
х₁ = -0,5(-2 - 6) = 4
х₂ = -0,5(-2 + 6) = -2
Итак мы получили ещё две точки параболы (4; 0) и (-2; 0).
Строим параболу (веточки её опущены вниз).
Смотри прикреплённый рисунок.
1) по графику видим, что функция убывает на интервале х ∈ [1; +∞)
2) множество решений неравенства 8 + 2x - x^2 ≤ 0 есть объединение двух интервалов х∈ (-∞; -2] ∪ [4; +∞)
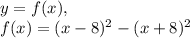
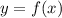— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 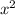(не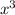 
, не 
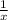, не 
и не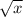 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид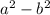 
, где 
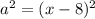, и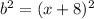 
. Формула «разность квадратов» раскрывается так: 
.
.
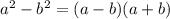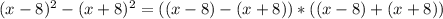
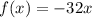, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Суффиксы а, л
Приставка по