Розв'язок:
Нехай швидкість автобуса — x км/год, тоді швидкість автомобіля — x+20 км/год.
Обидва автотранспорти проїхали одну і ту ж відстань — 30 км, але автомобіль був у дорозі на 15 хвилин менше від автобуса (виїхав пізніше на 10 хв і приїхав раніше на 5 хв).
Складе математичну модель і вирішимо її, врахувавши що 15 хв — це 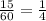 години.
години.
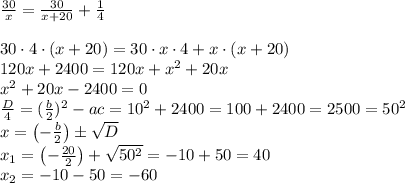
Значення х₂ відкидаємо, так як швидкість не може бути від'ємною.
Отже, швидкість автобуса — x = 40 км/год, а швидкість автомобіля — х+20 = 40+20 = 60 км/год.
Відповідь: Швидкість автомобіля 60 км/год.
(4;-5)
Або по іншому:
х = 4
у = -5
Объяснение:
Розписую пошагово. Якщо не зрозуміло , питайте..
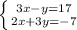 (в верхньому рівнянні знаходимо "у")
(в верхньому рівнянні знаходимо "у")
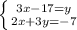 ( верхньому рівнянні перекинули "у" вправо, а 17 вліво змінивши на них знаки)
( верхньому рівнянні перекинули "у" вправо, а 17 вліво змінивши на них знаки)
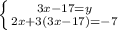 (підставляємо наш "у", який дорівнює (3х-17) в нижнє рівняння)
(підставляємо наш "у", який дорівнює (3х-17) в нижнє рівняння)
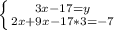 (розкриваємо дужки в нижньому рівнянні)
(розкриваємо дужки в нижньому рівнянні)
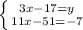 (вирішуємо нижнє рівняння)
(вирішуємо нижнє рівняння)
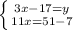
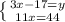
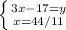
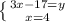
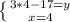 (підставляємо знайдений "х" в верхнє рівняння)
(підставляємо знайдений "х" в верхнє рівняння)
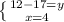
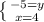
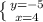
Перевіряємо підставляючи замість невідомих "х" та "у" знайдені числа::
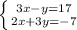
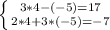
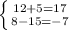
Тогда:
скорость, с которой катер плыл по течению = 10 + х км/ч
скорость, с которой катер плыл против течения = 10 - х км/ч
Тогда:
время, которое катер плыл по течению = 6 км / (10+х) км/ч = (6 / (10+х)) ч
время, которое катер плыл против течения = 10 км / (10-х) км/ч = (10/ (10-х)) ч
Разница между временами = 45 мин = 45 мин /60 мин/ч = (45/60) ч = (3/4) ч
Имеем уравнение
10/ (10-х) - 6/ (10-х) = 3/4
Г)