y(наиб) = 31 (в точке х = 2)
y(наим) = 5 (в точке x = 1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.
Найти все критические точки.
Проверить границы интервала.
Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8 - 4.
Приравниваем производную к 0:
8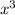 - 4 = 0
- 4 = 0
t = ±![\sqrt[3]{\frac{4}{3}}](/tpl/images/1201/1296/6cbb5.png) = ±
= ±![\sqrt[3]{\frac{1}{2}}](/tpl/images/1201/1296/97e2a.png) - однако, эти точки не входят в наш интервал.
- однако, эти точки не входят в наш интервал.
Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−4*1+7 = 5
x(2)=2*2^4−4*2+7 = 31
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
Разложим: (x-5)(x+5)