Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы 
. С другой стороны, как нетрудно заметить, их сумма равна 
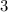. Стало быть, каждый из них равен единице: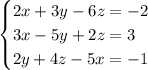 
Детерминант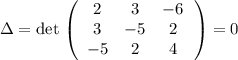 
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 
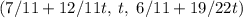, откуда 
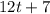должно делиться на 
, а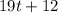 
должно делиться на 
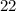. Тогда 
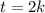, потому 
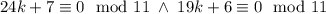. Из первого 
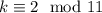, а из второго -- 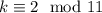. Итак, 
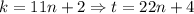, поэтому решение переписывается в виде 
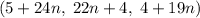. Итак, слева у исходного неравенства стоит нуль, а справа -- 
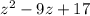. Получаем, что 
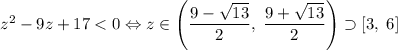, а потому подходит только 
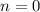и соответствующая тройка 
.
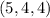Решим дискриминант и после этого сделаем метод интервала.
x²-3x-4 < 0
Дискриминант:
x²-3x-4 = 0
D = b²-4ac => (-3)²-4*1*(-4) = 9+16 = 25 > 0, 2 корня.
√25 = 5 (можно и в уме)
x =
x₁ =
x₂ =
Корни уравнения: (x+1)(x-4)
На графике будет выглядеть так:
-∞ + - + +∞
00>
-1 4 x
Воспользуемся методом интервала, чтобы понять, в какое направление пойдёт решение:
f (x) = (x+1)(x-4)
f (2) = (2+1)(2-4) = 3*(-2) = -6
ответ: (-∞;-1) ∪ (4;+∞).
