1) 3x-50
2) 2x^2-2x
Объяснение:
1) 5(x-8)-2(5+x)=5x-40-10-2x=3x-50
1. Здесь умножаем число на каждый одночлен в скобках
2. Получаем:
1) 5*x=5x
2) 5*(-8)=-40
3) (-2)*5=-10
4) (-2)*x=-2x
3. Складываем получившиеся одночлены: 5x+(-40)+(-10)+(-2x)=5x-40-10-2x
4. Приводим подобные слагаемые и получаем ответ: 5x-40-10-2x=5x-2x+(-40-10)=3x-50
2) x(x^2+x-2)-x^2(x-1)=x^3+x^2-2x-x^3+x^2=2x^2-2x
См. алгоритм 1
1) x*x^2=x^3 (степени складываются)
2) x*x=x^2 (см. 1)
3) x*(-2)=-2x
4) -x^2*x=-x^3
5) -x^2*(-1)=x^2
x^3-x^3+x^2+x^2-2x=2x^2-2x
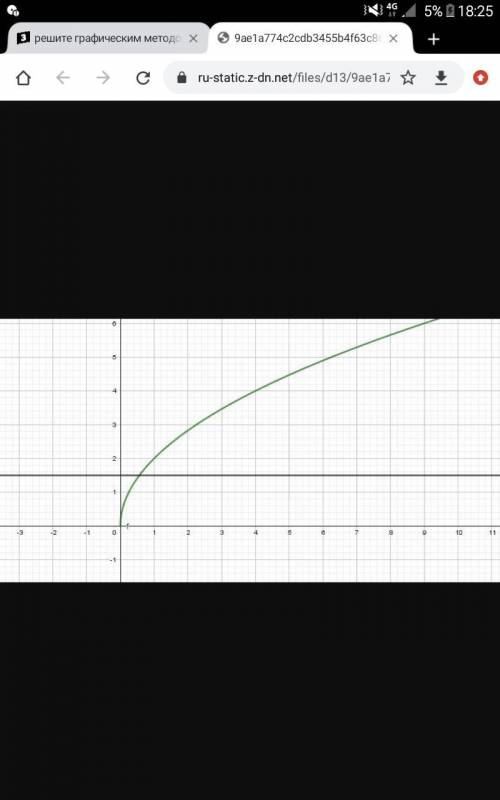
1) Построим графики функций и прямую параллельную оси ОХ
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
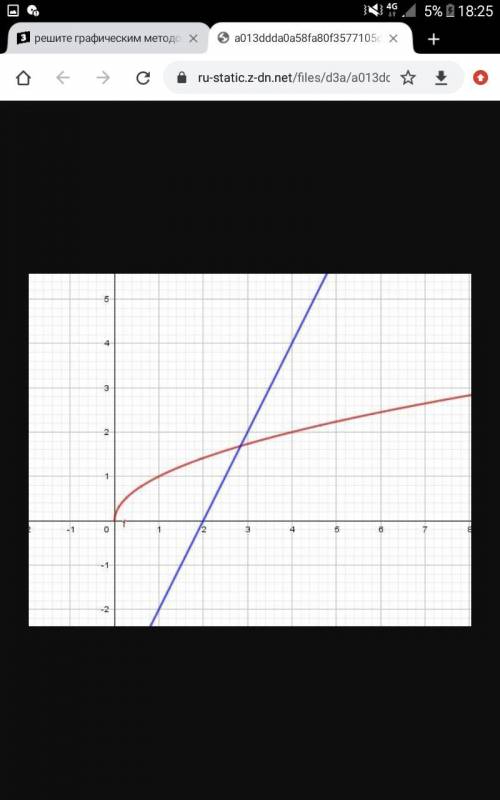
2) Построим график функции и прямую проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
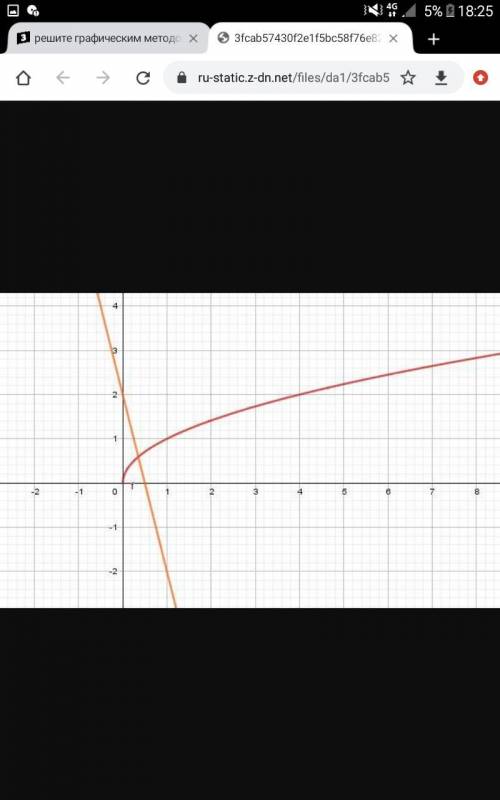
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна
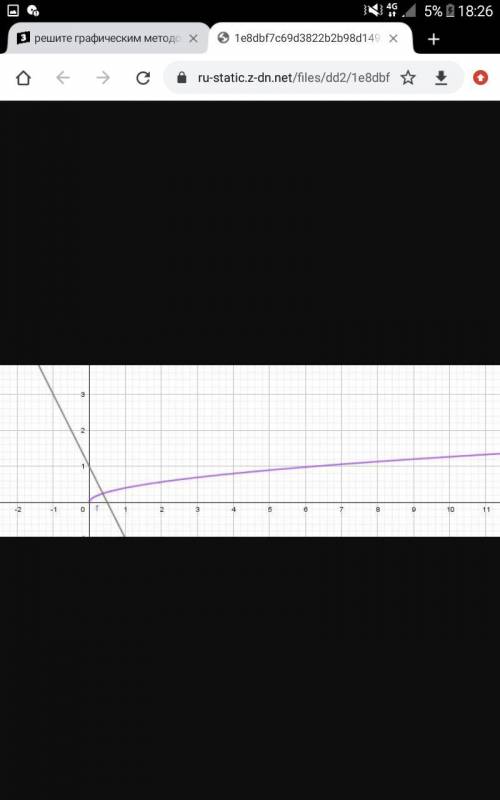
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна
15x=9
x=0,6
y=-10*0,6=-6