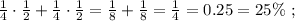Автомашина за 9 часов проходит 450 км расстояние найдите расстояние за 1 час

👇

Увидеть ответ

Ответ:

mishkateddi19

17.06.2022

450/9=50 (км) проходит машина за час

4,4(79 оценок)

Ответ:

авлвк5

17.06.2022

Составим пропорцию и найдем расстояние, которое автомашина проходит за час:
[время-расстояние]
9-450
1-х
9х=450
х=450/9
х=50
ответ: за час автомашина проходит 50 км.

4,8(93 оценок)

Открыть все ответы

Ответ:

JaanB

17.06.2022

1. 1) (c - 6)2 = 2c - 12.

3) (5 - a)(5 + a) = 25 - a^2.

2) (2a - 36)2 = 4a - 72,

4) (7x + 10y)(10y - 1x) = 70xy - 7x^2 + 100y^2 - 10xy^2,

2. 1) ь? - що це?

3) 100 - 9x^2 = (10 - 3x)(10 + 3x).

2) c? - а це що?

4) 4a + 20ab + 25b^2 = (2a + 5b)^2 (напевно там повинно бути 4a^2)

1 варіант

4(3y + 1)^2 - 27 = (4y + 9)(4y - 9) + 2(5y + 2)(2y - 7)

4(9y^2 + 6y + 1) - 27 = 16y^2 - 81 + 2(10y^2 - 35y + 4y - 14)

36y^2 + 24y + 4 - 27 = 16y^2 - 81 + 20y^2 - 70y + 8y - 28

36y^2 + 24y - 16y^2 - 20y^2 - 70y + 8y = 27 - 4 - 81 - 28

54y = - 29

y = - 29 / 54

2 варіант

4(3y + 1)^2 - 27 = (4y + 9)(4y - 9) + 2(5y + 2)(2y - 7)

4 * 9y^2 + 6y + 1 - 27 = 16y^2 - 81 + 2 * 10y^2 - 35y + 4y - 14

36y^2 + 6y + 1 - 27 = 16y^2 - 81 + 20y^2 - 35y + 4y - 14

36y^2 + 6y - 16y^2 - 20y^2 + 35y - 4y = 27 - 1 - 81 - 28

37y = - 83

y = - 83 / 37

y = - 2 9/37

Напишіть хтось, який правильний. Може десь є помилка.

5, 6 - що це за знаки питання?

4,7(4 оценок)

Ответ:

Danfdffefd

17.06.2022

Исходное неравенство распадается на совокупность систем:

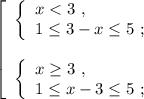
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

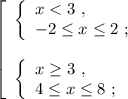
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

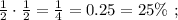
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

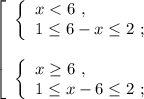
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

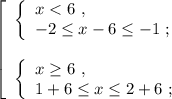
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...

Образование

05.08.2020

Решить систему уравнений x2 + xy +y2 = 13...

Образование