Алгебра: Решите тригонометрическое уравнение

Копирую часть своего ответа, А САМО РЕШЕНИЕ В КОНЦЕ Разделить число a на число b означает узнать, из какого количества (из со скольких штук) числа (чисел) b можно составить число a Из шести троек (если сложить их все) можно составить число 18. Хорошо, теперь интересное: сколько нулей нужно добавить, что бы получилась единица? ответа не существует. Другими словами как я могу разделить один миллион евро среди 0-ля людей? А ни как, людей нету. Т.е. в этом случае операция деления на ноль просто напросто...

Решите тригонометрическое уравнение

👇

Увидеть ответ

Ответ:

amalia454565

25.05.2020

В знаменателе применим формулу приведения:
4tg²x - 3/cosx + 3 = 0
Умножим на cos²x:
4sin²x - 3cosx + 3cos²x = 0
4(1 - cos²x) - 3cosx + 3cos²x = 0
cos²x + 3cosx - 4 = 0
cosx = t
t² + 3t - 4 = 0
D = 9 + 16 = 25
t = 1 t = - 4
cosx = 1 cosx = - 4
x = 2πn нет корней

4,5(17 оценок)

Открыть все ответы

Ответ:

Annsad12121

25.05.2020

1-е число равно 2, 3-е число равно 0.4.

Объяснение:

Обозначим через x1 первое число из трех данных чисел.

В исходных данных к данному заданию сообщается, что 1-е число впятеро больше, чем 3-е, следовательно, 3-е число должно составлять х1/5.

Также известно, что три данных числа являются арифметической прогрессией.

Следовательно, полусумма 1-го и 3-го чисел должна быть равна 2-му числу и мы можем составить следующее уравнение:

(х1 + х1/5) / 2 = 1.2,

решая которое, получаем:

(6х1/5) / 2 = 1.2;

3х1/5 = 1.2;

х1/5 = 1.2 / 3;

х1/5 = 0.4;

х1 = 0.4 * 5 = 2.

Находим 3-е число:

х1/5 = 2/5 = 0.4.

4,6(24 оценок)

Ответ:

hihilaim

25.05.2020

Копирую часть своего ответа, А САМО РЕШЕНИЕ В КОНЦЕ

Разделить число a на число b означает узнать, из какого количества (из со скольких штук) числа (чисел) b можно составить число a

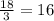$\frac{18}{3}=16$ Из шести троек (если сложить их все) можно составить число 18.

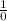Хорошо, теперь интересное: $\frac{1}{0}$ сколько нулей нужно добавить, что бы получилась единица? ответа не существует. Другими словами как я могу разделить один миллион евро среди 0-ля людей? А ни как, людей нету. Т.е. в этом случае операция деления на ноль просто напросто не несет никакой информационной нагрузки.

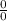Хорошо. а как быть с $\frac{0}{0}$ ?

0 можно получить добавив 2 нуля, 4, сколько хочешь нулей, ни сколько нулей, кажется ответ должен быть, и так можно делать с числами.
Тут нужно вспомнить, что ответом для операции деления одного числа на другое люди договорились считать одно ЕДИНСТВЕННОЕ число, а тут у нас неоднозначность, не один ответ, т.е. такая операция тоже не задана.

Также, под корнем не может быть отрицательного числа, т.е. выражение под корнем должно быть большим или равным нулю. В силу того, как вводится понятие корня квадратного, в силу определения корня квадратного.
Если корень стоит в знаменателе, то подкоренное выражение должно быть уже строго большим за 0.

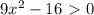
$9x^2-16\ \textgreater \ 0$
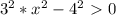
$3^2*x^2-4^2\ \textgreater \ 0$
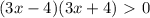
$(3x-4)(3x+4)\ \textgreater \ 0$
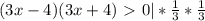
$(3x-4)(3x+4)\ \textgreater \ 0|* \frac{1}{3}* \frac{1}{3}$
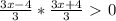
$\frac{3x-4}{3} * \frac{3x+4}{3}\ \textgreater \ 0$
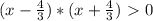$(x- \frac{4}{3}) *(x+ \frac{4}{3})\ \textgreater \ 0$ (*)

Два случая (две возможности):
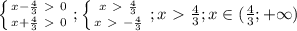
1) $\left \{ {{x- \frac{4}{3}\ \textgreater \ 0} \atop {x+ \frac{4}{3}\ \textgreater \ 0}} \right. ;
 \left \{ {{x\ \textgreater \ \frac{4}{3}} \atop {x\ \textgreater \ - \frac{4}{3}}} \right. ;
x\ \textgreater \ \frac{4}{3};
x\in(\frac{4}{3};+\infty)$

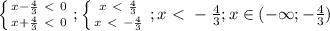
2) $\left \{ {{x- \frac{4}{3}\ \textless \ 0} \atop {x+ \frac{4}{3}\ \textless \ 0}} \right. ;
 \left \{ {{x\ \textless \ \frac{4}{3}} \atop {x\ \textless \ - \frac{4}{3}}} \right. ;
x\ \textless \ - \frac{4}{3};
x\in(-\infty;-\frac{4}{3})$

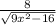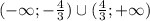
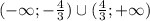
Т.е. неравенство (*) превращается в правдивое числовое (и одновременно с этим имеет смысл выражение $\frac{8}{ \sqrt{9x^2-16} }$ ) при значениях х-са из промежутка: $(-\infty; -\frac{4}{3} )\cup(\frac{4}{3};+\infty)$

ответ: $(-\infty; -\frac{4}{3} )\cup(\frac{4}{3};+\infty)$

4,5(11 оценок)

Это интересно:

Компьютеры-и-электроника

09.12.2022

Как взломать Wi-Fi сеть (WEP) с помощью Airoway и Wifislax...

Образование-и-коммуникации

08.01.2020

Как стать интересным: советы и рекомендации...

Образование-и-коммуникации

28.08.2021

Как написать описательный абзац: эффективные советы и примеры...

Здоровье