1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a - b)2 = a2 - 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 - b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a - b)3 = a3 - 3a2b + 3ab2 - b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 - ab + b2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 - b3 = (a - b) (a2 + ab + b2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) (40+1)2
б) 982
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1)2 = 402 + 2 · 40 · 1 + 12 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
982 = (100 – 2)2 = 1002 - 2 · 100 · 2 + 22 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Решение
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х - у)2 + (х + у)2
Решение
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х - у)2 + (х + у)2 = х2 - 2ху + у2 + х2 + 2ху + у2 = 2х2 + 2у2
Формулы сокращенного умножения в одной таблице:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
a2 - b2 = (a - b) (a+b)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
a3 + b3 = (a + b) (a2 - ab + b2)
a3 - b3 = (a - b) (a2 + ab + b2)
При x>0 функция в левой части возрастает, а функция в правой части убывает, значит их графики пересекаются лишь в одной точке, ясно что эта точка - x=25. При этом очевидно, что всюду ЛЕВЕЕ этой точки график функции 27-x лежит выше графика функции логарифма на координантной плоскости. Ну ясно же, один график шел снизу вверх (логарифм), а другой сверху вниз (27-x), в этой точке они пересеклись и для x>25 уже наоборот график логарифма будет лежать выше.
Поэтому ответ: 0<x≤25
"Расписать подробно":
Функция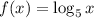 
определена при x>0 и монотонно возрастает, так как основание логарифма больше 1.
Функция g(x)=27-x убывает, так как (27-x)'=-1
x=25 - корень уравнения f(x)=g(x). Причем корень единственный, это следует из выше написанного.
Тогда очевидно, что f(x)≤g(x) при 0<x≤25
P.S.
Функции тут простые, поэтому можно вообще забить на аналитическое решение и его обоснование, а решить графически. Начертить графики и на чертеже сразу будет видно то, что аналитически приходится доказывать с свойств функций.
находим площадь с определенного интеграла:
ответ: