и 
. Чтобы найти координату 
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
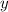можем найти подставив в выражение первой функции , а можно сделать проще. Так как пересечение будет с прямой , то и точки пересечения будут иметь координату . Итак, получилось две точки пересечения с координатами: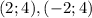 
.![[0;1]](/tpl/images/0561/5883/90495.png)
(этот отрезок по оси ), найдем значения 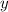на концах этого отрезка: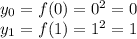
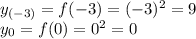
Найдем производную функции, приравняем ее к нулю, найдем критические точки, разобьем числовую ось ими на интервалы, установим на каждом из них знаки, если при переходе через критич. точку производная меняет знак с минуса на плюс, то это точка максимума, с плюса на минус - точка минимума.
производная -8/х³-1=0, откуда х=-2, При переходе через точку х=-2 произвдоная меняет знак с минуса на плюс, значит, х=-2- точка минимума, при переходе через точку х=0 производная меняет знак с плюса на минус, но х=0- не входит в область определения, поэтому не может быть точкой экстремума.
a(1)=v'=-π²/16*sinπ/4=-π²/16*√2/2=-√2*π²/32