1. а) 5xy³*(-2x²y)⁴ = 5xy³*16x⁸y⁴ = 80x¹⁺⁸y³⁺⁴ = 80x⁹y⁷
б) (2y-3x)² - (3x+2y)(2y-3x) = 4y²-12xy+9x²-6xy-9x²+4y²-6xy = 8y²-24xy
2. а) 4ab³-a³b = ab (4b²-a²) = ab (2b-a)(2b+a)
б) -9b-6b²-b³ = -b (9+6b+b²) = -b (b+3)²
3. 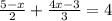
Здесь делаем всем НОЗ: 6.
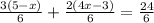
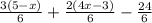
Теперь, когда у нас стали одинаковые знаменатели, решаем только числитель:
3(5-x)+2(4x-3)-24 = 0
15-3x+8x-6-24 = 0
-3x+8x+15-6-24 = 0
-5x-13 = 0
-5x = 13
x = -2,6
4. Увы, задачу не понял.
5. y = 4x-7 - линейная функция, графиком является прямая.
y = x+83 - линейная функция, графиком является прямая.
Построим таблицы:
1) y = 4x-7
x | 0 1
y | -7 -3
y₁ = 4*0-7 = -7
y₂ = 4*1-7 = -3
2) y = x+83
x | 0 1
y | 83 84
y₁ = 0+83 = 83
y₂ = 1+83 = 84
Как строить координатную плоскость - думаю, не надо объяснять.
Для любого x из области определения функции f(x) верно следующее: f(x)=-f(-x). Это определение нечётной функции, из этого следует, что область определения должна быть симметричной относительно нуля, ведь каждому x>0 соответствует такой -x<0, что f(x)=-f(-x).
а) [-5;-3)U(3;5) этот промежуток не может являться областью определения т.к. -5 включается, а 5 не включается (для x=-5 не существует -x=5).
б) (-∞;0) U (0; +∞) здесь симметрия соблюдается.
в) [-8; 7] этот промежуток не может явл. обл. опр. т.к. -8 включается, а 8 не включается (для x=-8 не существует -x=8).
г) (-1;1) симметрия соблюдается.
ответ: а) [-5;-3)U(3;5)
в) [-8; 7]
.