![Найдите наибольшее значение функции f (x) = -x^3 + 3x^2 +9x -29 на отрезке [ -1; 4 ]. в ответе должн](/tpl/images/0775/7454/1dda2.jpg)
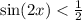
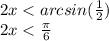
разделим обе стороны на 2 чтоб упростить
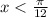
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из
π
, чтобы найти решение во втором квадранте.
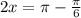
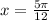
Период функции
sin(2х)
равен
π
, то есть значения будут повторяться через каждые
π
радиан в обоих направлениях
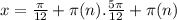
для всех целых n
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
1.
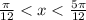
1 это ложно
2.
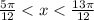
2 это истинно
3.
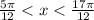
3 это ложно.
Итак
решение включает все истинные интервалы:
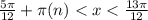
для всех целых n
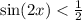
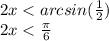
разделим обе стороны на 2 чтоб упростить
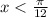
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из
π
, чтобы найти решение во втором квадранте.
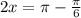
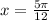
Период функции
sin(2х)
равен
π
, то есть значения будут повторяться через каждые
π
радиан в обоих направлениях
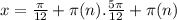
для всех целых n
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
1.
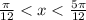
1 это ложно
2.
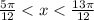
2 это истинно
3.
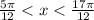
3 это ложно.
Итак
решение включает все истинные интервалы:
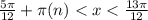
для всех целых n
f(x) = -x³ +3x² +9x - 29
f'(x) = -3x² + 6x + 9
-3x² + 6x + 9 = 0 | : (-3)
x² - 2x - 3 = 0
по теореме виетта:
x₁ = -1
x₂ = 3
f(-1) = - (-1)³ + 3 (-1)² + 9 (-1) - 29 = 1 + 3 - 9 - 29 = -34
f(3) = -2
f(4) = -9
ответ: наибольшее значение -2