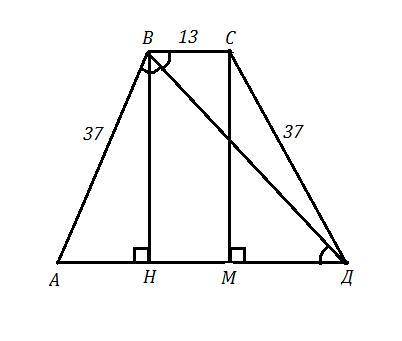
АВСД - трапеция , АВ=СД=37 см , ВС=13 см , ВД - биссектриса ∠В .
Так как ВД - биссектриса ∠В , то ∠АВД=∠СВД .
Так как ВС║АД и ВД - секущая, то ∠СВД=∠АДВ как внутренние накрест лежащие углы, и тогда ∠АВД=∠АДВ ⇒ ΔАВД - равнобедренный, АВ=ВД=37 см .
Проведём ВН⊥АД и СМ⊥АД . ВСМН - прямоугольник и МН=ВС=13 см
АН=МД=37-13=24 см , АН=МД=24:2=12 см .
Рассмотрим ΔАВН .
По теореме Пифагора ВН=√(АВ²-АН²)=√(37²-12²)=√1225=35 см .
ВН - высота трапеции.
Площадь трапеции:
S=(АД+BC)/2*ВН=(37+13)/2*35=50/2*35=25*35=875 см²
решу систему методом подстановки.
1) выразим х через второе уравнение:
х= (5-7у)\3
2) подставляешь в 1 уравнение вместо х получившееся выражение:
4* (5-7у)\3 -5у=-22
(20-28у)\3-5у=-22
перегоним все в левую часть:
(20-28у)\3-5у+22=0
подгоним все под общий знаменатель 3:
(20-28у-15у+66)\3=0
3) дробь равна 0, когда числитель равен 0, а знаменатель не равен. значит отбрасываем знаменатель. НО. на 0 делить нельзя, значит нельзя, чтобы в знаменателе получился 0. но тут нас устроит любое значение х, тк х нет в знаменателе. решаем:
-43у+86=0
43у= 86
у= 86\43
4) подставляем во 2 уравнение вместо у получившееся:
3х+ 7* 86\43=5
3х+ 608\43-5=0
подгоняем под общий знаменатель:
(129х+608-215)\43=0
тоже самое, что и в 3 действии:
129х= -393
х= - 393\129= -131\43
1,5a = 2; a = (1)1/3. Теперь подставим вместо икса 0 и найдём b:
b = 1,5 * 0 - 2; b = -2; a + b = (1)1/3 - 2 = - 2/3