2
Объяснение:
x - скорость течения, км/ч.
y - время, затраченное по течению, ч.
Система уравнений:
(y+0,5)(14-x)=24; 14y-xy+7-0,5x=24; 14y-xy-0,5x=17
y(14+x)=24; 14y+xy=24
14y-xy-0,5x+14y+xy=17+24
28y-0,5x=41 |×2
x=56y-82
y(14+56y-82)=24
56y²-68y-24=0 |4
14y²-17y-6=0; D=289+336=625
y₁=(17-25)/28=-8/28=-2/7 - ответ не подходит по смыслу.
y₂=(17+25)/28=42/28=3/2=1,5 ч потребовалось пройти путь лодке по течению.
3/2 ·(14+x)=24
14+x=24·2/3
x=8·2-14
x=2 км/ч - скорость течения.
x^2 - 3x + 2 = (x - 1)(x - 2) < 0
Решением этого неравенства является промежуток (1, 2)
Разложим на множители левую часть второго неравенства:
ax^2 - (3a + 1)x + 3 = (ax^2 - x) - (3ax - 3) = x(ax - 1) - 3(ax - 1) = (x - 3)(ax - 1) = a(x - 3)(x - 1/a)
Возможны 5 вариантов.
1) a > 1/3. Тогда решение неравенства – промежуток (1/a, 3). Нужно, чтобы промежуток (1, 2) полностью содержался в нём, так будет, если 1/a < 1. Объединяем с условием a > 1/3 и получаем часть ответа: a > 1.
2) a = 1/3. У второго неравенства нет решений.
3) 0 < a < 1/3. Решение неравенства – промежуток (3, 1/a); такой промежуток никогда не содержит (1, 2).
4) a = 0. Второе неравенство превращается в 3 - x < 0, x > 3. Не подходит.
5) a < 0. Решение второго неравенства – промежуток (1/a, 3), при этом 1/a < 0. Подходит.
ответ. 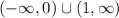
(a²+b²)-(a²+b²-1)
ab²-ab²-1
ab-ab⁴-1
ab-ab⁴-¹
ab+ab³