6543 и 6210
Объяснение:
Рассматриваются четырёхзначные числа M, среди которых нужно выбрать числа, удовлетворяющие условиям:
1) 6000 < M < 7000;
2) M делится на 9;
3) каждая следующая цифра M меньше предыдущей.
Если представить число M в виде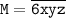 
, где хотя-бы один из цифр x или y или z отличен от 0, то 1-условие выполнено. Но, если выполняется 3-условие, то есть если 6>x>y>z, то 1-условие выполняется.
Рассмотрим все числа вида 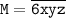, для которых выполнено 3-условие:
6543, 6542, 6541, 6540, 6532, 6531, 6530, 6521, 6520, 6510;
6432, 6431, 6430, 6421, 6420, 6410;
6321, 6320, 6310;
6210.
Остается проверить 2-условие для этих чисел. Используем признак делимости на 9:
Число А делится на 9 ⇔ Сумма цифр числа А делится на 9.
Нетрудно проверить, что только следующие числа делятся на 9:
6543 (6+5+4+3=18) и 6210 (6+2+1+0=9).
Пусть b1,b2,,bn, - члены прогрессии, а q - её знаменатель. Сумма прогрессии S=b1/(1-q). По условию, b1/(1-q)=6. Одновременно по условию S1=b1²+b2²++bn²+=12. Но S=b1*(1+q+q²+q³), а S1=b1²*(1+q²+q⁴+q⁶+). Получена система уравнений:
b1*(1+q+q²+q³)=6
b1²*(1+q²+q⁴+q⁶+)=12
Возведём первое уравнение в квадрат:
b1²*(1+q+q²+q³)²=36
b1²*(1+q²+q⁴+q⁶+)=12
Разделив теперь первое уравнение на второе, придём к уравнению относительно q: (1+q+q²+q³+)²/(1+q²+q⁴+q⁶+)=3. Но в скобках числителя - бесконечная геометрическая прогрессия со знаменателем q, её сумма S2=1/(1-q). В скобках знаменателя - бесконечная геометрическая прогрессия со знаменателем q², её сумма S3=1/(1-q²). Отсюда следует уравнение (1-q²)/(1-q)²=3, которое приводится к квадратному уравнению 2*q²-3*q+1=0. Решая его, находим q1=1 и q2=1/2. Но при q=1 сумма прогрессии была бы равна бесконечности, поэтому q=1/2. ответ: 1/2.
Б)9⁶*9=9⁷
В) b ⁵ * b ⁶=b¹¹
Г)(2a)³ * (2а)⁴=(2*a)⁷
Д)с ³ с ⁴ с ⁸=c¹⁵
Е)а ² а ⁹ а=a¹²