6
Объяснение:
Область определения функции: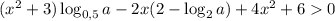 
. Неравенство должно выполняться для любого x, в частности для x = 0. Подставим это значение:
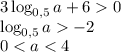
Значит, потенциально подходящие значения a = 1, 2, 3. Необходимо проверить каждое из них, чтобы удостовериться, что неравенство справедливо для всех x. Приведём левую часть к стандартному виду квадратного трёхчлена:
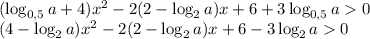
Так как a не превосходит 3, старший коэффициент положителен, ветви параболы направлены вверх. Значит, чтобы неравенство выполнялось для всех x, дискриминант левой части (или в данном случае удобно использовать D/4) должен быть отрицательным:
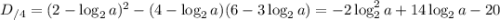
Пусть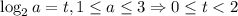 
.
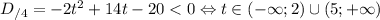
Все t подходят, а значит, и все a. Сумма подходящих a — 1 + 2 + 3 = 6.
-18; 16
Объяснение:
Возможен графический вариант
решения:
1.
Разбиваем неравенство на две
части:
(Х+18)^1/2+Х<=2
(Х-18)^1/2<=-Х+2
2.
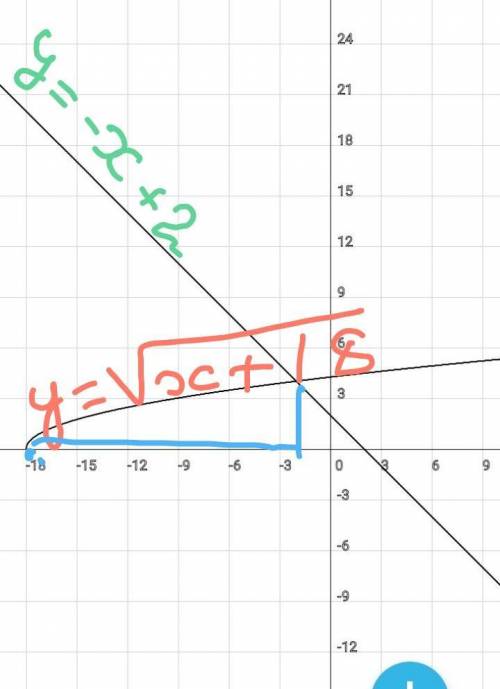
Строим график функции
У=(Х+18)^1/2
3.
В этой же системе координат
строим график прямой
У=-Х+2
4.
По графику определяем про
межуток, в котором график
функции У=(Х+18)^1/2 прохо
дит ниже прямой У=-Х+2, или
пересекается с ней ( так как
неравенство нестрогое).
5.
Результат графического ре
шения:
Х€[-18; -2]
6.
Наименьшее значение Х=-18
7.
Длина наибольшего интерва
ла, входящего во множество
решений:
|-18-(-2)|=16(ед.)
330*0,3=99кг картофеля