Объяснение:
1 = a
-5 = b
-36 = c
D= b^2 - 4ac
D= 25 - (4 * 36) = 169
x1 = -b + √D/2a (/ это дробная черта)
x2= -b - √D/2a
x1 = 5+13/2*1 = 9
x2= 5 -13/2*1 = -4
ответ : x1 = 9 ; x2 = -4
Чтобы определить проходит ли график функции через данные точки, нужно координаты этих точек подставить в уравнение функции и проверить, выполняется ли равенство.
у=3х²-х-2
А (-1; 2)
2=3*(-1)²-(-1)-2
2=3+1-2
2=2
Равенство верно, следовательно график функции проходит через точку А.
В (2; 8)
8=3*2²-2-2
8=12-4
8=8
Равенство верно, следовательно график функции проходит через точку В.
С (0;3)
3=3*0²-0-2
3=-2
Равенство неверно, следовательно график функции не проходит через точку С.
D (1; 4)
4=3*1²-1-2
4=3-3
4=0
Равенство неверно, следовательно график функции не проходит через точку D.
ответ: график функции у=3х²-х-2 проходит через точку А (-1; 2) и В (2; 8).
Объяснение:
Теоремой Виета было бы проще.
D = b^2 - 4*a*c = 5^2 + 4*(1*36) = 25 + 144 = 169
Для поиска корней уравнения берём корень из дискриминанта:
Далее ищем корни уравнения:
1) (-b +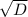 )/2a = (5 + 13) /2 = 18/2 = 9
)/2a = (5 + 13) /2 = 18/2 = 9
2) (-b -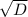 )/2a = (5 - 13) /2 = -8/2 = -4
)/2a = (5 - 13) /2 = -8/2 = -4
В уравнении 2 корня, так как уравнение второго порядка.