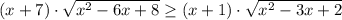
ОДЗ:
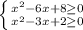
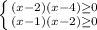⇒ ![x \in (-\infty; 1] \cup 2 \cup [4; +\infty)](/tpl/images/1358/6177/43eb1.png)
Рассматриваем четыре случая с учетом ОДЗ:
1) Если правая часть неотрицательна, левая неположительна
⇒ 
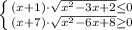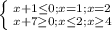⇒![x \in [-7;- 1]](/tpl/images/1358/6177/6a83a.png)
U{1} U {2}
Неравенство верно при любых ![x \in [-7;-1]](/tpl/images/1358/6177/c74ad.png)
U {1} U {2}
2)
Если правая часть отрицательная, левая неотрицательная, неравенство неверно:
⇒ 
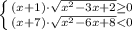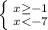⇒ нет таких значений х
3)
Если правая часть неотрицательная , левая неотрицательная
⇒ 
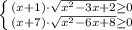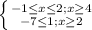⇒ ![x \in [-1;1] \cup2\cup[4;+\infty)](/tpl/images/1358/6177/31cdc.png)
возводим обе части неравенства в квадрат:
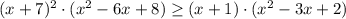
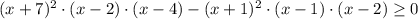
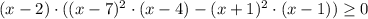
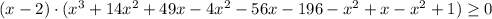
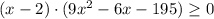
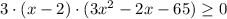D=(-2)²-4·3·(-65)=784=28²
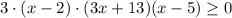
![x \in [-\frac{13}{3} ;2] \cup[5;+\infty)](/tpl/images/1358/6177/cbf3a.png)
C учетом условия третьего случая: ![x \in [-1;1] \cup[4;+\infty)](/tpl/images/1358/6177/0dfc8.png)
получим ответ третьего случая ![x \in [-1;1] \cup [5;+\infty)](/tpl/images/1358/6177/97b92.png)
4)
Если левая часть отрицательная и правая тоже отрицательна
⇒ 
⇒ 
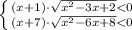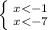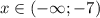
умножаем на (-1) обе части неравенства и
возводим в квадрат:
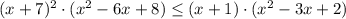
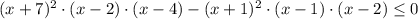
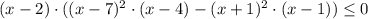
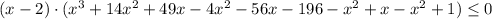
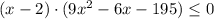
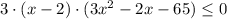
D=(-2)²-4·3·(-65)=784=28²
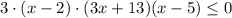
![x \in (-\infty;-\frac{13}{3} ] \cup [2;5]](/tpl/images/1358/6177/2eb9e.png)
C учетом условия четвертого случая: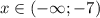
получим ответ четвертого случая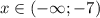
Объединяем ответы рассмотренных случаев:
![x \in (-\infty;1] \cup 2 \cup [5;+\infty)](/tpl/images/1358/6177/e399f.png)
Все в объяснениях.
Объяснение:
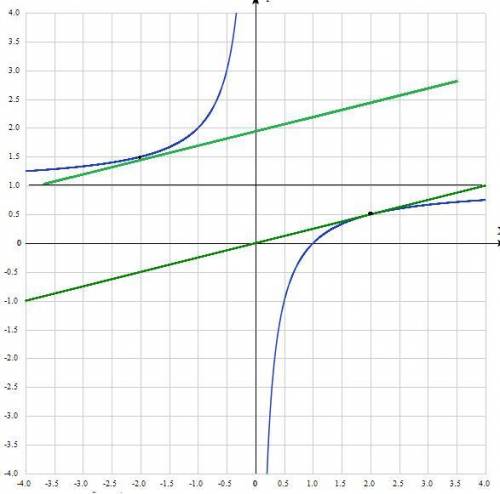
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=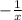
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (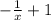 
) ' =
.
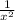3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=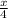
, к=1\4.
Найдем точку касания
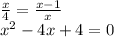
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х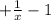
)' =
=1 -=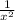
.
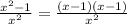у'=0 ,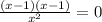 
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =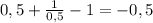
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5
