По свойству арифметической прогрессии:
, где d-это разность арифметической прогрессии.
Из условий можно составить систему из 2х уравнений:
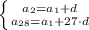
нам известно что: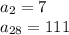 
Подставляем и получаем:
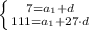
Решаем систему: из 1го уравнения выражаем ну хотя бы d:
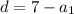
Подставляем во второе:
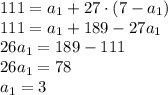
Теперь найдем d:
Разность прогрессии нашли, она равна 4.
Теперь сумма первых 28 членов:
По формуле сумма n членов арифметической прогрессии равна:
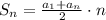или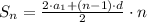 
Можно пользоваться любой формулой результат будет одинаковый, но воспользуемся все таки первой, она проще для вычислений и 28 член прогрессии нам известен.
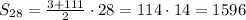
(можно убедиться, что вторая формула даст такой же результат).
разность арифметической прогрессии d = 4
Сумма первых 28 членов прогрессии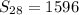 
11n + 7, где n - целое неотрицательное число.
Объяснение:
Целое число, кратное 11, имеет вид 11n, где ∈ Z ( n - целое число), тогда формула целого числа,которое при делении на 11 даёт остаток 7, примет вид
11n + 7.
В нашей задаче речь не о целых, а о натуральных числах. Из всего множества целых чисел n мы в ответе должны оставить лишь те, которые дадут натуральное число 11n + 7.
При n = 0 получим наименьшее натуральное число, равное 7. Действительно, 7 : 11 = 0 (ост. 7)
Получили, что формула натурального числа, которое при делении на 11 даёт остаток 7, выглядит так:
11n + 7, где n - целое неотрицательное число.
(n = 0; n = 1; n = 2 и т.д)
чем в 1-ой цистерне.
За t мин из 1 цистерны выльется 25t л воды, а из второй 30t л воды.
Останется в 1-ой цистерне (700-25t) л воды,
а во 2-ой: (340-30t) л воды, что в 5 раз меньше, чем (700-25t).
Уравнение:
700-25t=5*(340-30t)
700-25t=1700-150t
125t=1000
t=8
ответ: через 8 мин .