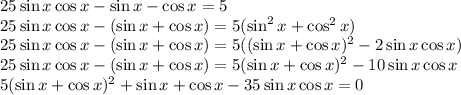
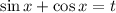 , тогда
, тогда 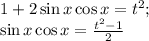 , имеем
, имеем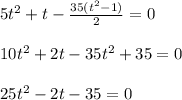
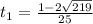
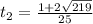
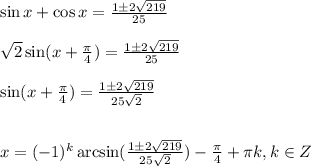
ответ: 3) а) а фигурасын (0; 3) нүктесіне қарағанда 180° бұрыңыз және шыққан фигураны в деп белгілеңіз;
б) а фигурасын центрге қарағанда симметриялы бейнелеңіз және шыққан фигураны с деп
белгілеңіз;
c) a фигурасын (3; 2) векторына параллель көшіріңіз және шыққан фигураны d деп белгілеңіз.
3) а) а фигурасын (0; 3) нүктесіне қарағанда 180° бұрыңыз және шыққан фигураны в деп белгілеңіз;
б) а фигурасын центрге қарағанда симметриялы бейнелеңіз және шыққан фигураны с деп
белгілеңіз;
c) a фигурасын (3; 2) векторына параллель көшіріңіз және шыққан фигураны d деп белгілеңіз.
ответ: ('-')
_стройте быстрее ! |__/
('_') / | |
_|_ | y = v / \
| |
/ \ || x+2
/ { -1; 7 }
('_')_/ /
|__/
|
/ \
Решить уравнение
25*sin(x)cos(x)-sin(x)-cos(x)=5 ;
25*( ( sin(x) +cos(x) )² - 1) /2 - ( sin(x) +cos(x) =5 ;
замена: t = sin(x) +cos(x) = √2cos(x -π/4) ; -√2 ≤ √2cos(x -π/4) ≤ √2
25(t² -1)/2 - t =5 ;
25t² -2t -35 =0 ; D₁ =(2/2)² - 25*(-35) =1 +875 =876 =(2√219)²
t₁ = (1 -2√219) / 25 ;
t₂ = (1+2√219) / 25 .
* * * t₁ и t₂ ∈ [ - √2 ; √2] * * *
a)
√2cos(x -π/4) = (1 -2√219) / 25 ;
cos(x -π/4) = √2(1 -2√219) / 50
x -π/4 = ± arccos (√2(1 -2√219) / 50) +2πn , n ∈ Z .
x = π/ 4 ± arccos (√2(1 -2√219) / 50) +2πn , n ∈ Z .
б)
√2cos(x -π/4) = (1 +2√219) / 25;
x = π/ 4 ± arccos (√2(1 +2√219) / 50) +2πn , n ∈ Z .√2