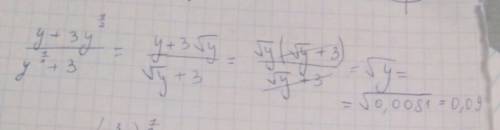
Объяснение:
Пусть Х часов - время, которое необходимо первому рабочему для выполнения задания.
Тогда время выполнения вторым рабочим равно (Х + 4) часов.
2. Обозначим все задание за 1.
Тогда производительность первого рабочего 1/Х ед/час, второго - 1/(Х + 4) ед/час.
3. По условию задачи сначала первый рабочий работал 2 часа.
Тогда он выполнил 2 * 1/Х = 2/Х часть задания.
Затем второй рабочий работал 3 часа и выполнил 3 * 1/(Х + 4) = 3/(Х + 4) часть задания.
4. Вместе они сделали 1/2 часть работы.
2/Х + 3/(Х + 4) = 1/2.
4 * Х + 16 + 6 * Х = Х * (Х + 4).
Х * Х - 6 * Х - 16 = 0.
Дискриминант D = 6 * 6 + 4 * 16 = 100.
Х = (6 + 10) / 2 = 8 часов - время первого рабочего.
Х + 4 = 8 + 4 = 12 часов - второго.
ответ: За 8 часов может выполнить задание первый рабочий и за 12 часов - второй.
1) Найдите значение выражения:
1,5·62-23=93-23=70;
2) Представьте в виде степени выражение:
а) x⁸∙x²=x⁸⁺²=x¹⁰;
б) x⁸:x²=x⁸⁻²=x⁶;
в) (x⁸)²=x⁸ˣ² =x¹⁶.
3) Преобразуйте выражение в одночлен стандартного вида:
a) -6∙a³∙b⁷∙5∙a²∙b= -30∙a³⁺²∙b⁷⁺¹ = -30∙a⁵∙b⁸;
b) (-7∙a⁴∙b⁶)³= -343∙a⁴ˣ³∙b⁶ˣ³= -343∙a¹²∙b¹⁸.
4) Представьте в виде многочлена стандартного вида выражение (15∙x²-6∙х-3)-(2∙x²-23∙x-44)=15∙x²-2∙x²-6∙х+23∙x+44-3= 13∙x²+17∙х+41.
Задания 5) нет в условии!
6) Упростите выражение:
125·a⁶·b³∙(-0,2·a²·b⁴)³ = 125·a⁶·b³∙(-0,008)·a²ˣ³·b⁴ˣ³ = -1·a⁶·b³·a⁶·b¹² =
= -a⁶⁺⁶·b³⁺¹² = -a¹²·b¹⁵.
7) Вместо звездочки напишите такой многочлен, чтобы образовалось тождество:
(5·a³-2·a·b+6·b)-(*)=4·a³+8·b ⇒ * = (5·a³-2·a·b+6·b)-(4·a³+8·b)=
=5·a³-2·a·b+6·b-4·a³-8·b= a³-2·a·b-2·b.
8) Докажите, что значение выражения (3·n+16)-(6-2·n) кратно 5 при любом натуральном значении n.
(3·n+16)-(6-2·n)=3·n+16-6+2·n=5·n+10= 5·(n+2).
Так как в последнем выражении участвует множитель 5, то
(3·n+16)-(6-2·n)=5·(n+2) кратно 5 при любом натуральном значении n.
9) Известно, что 2·a²·b³=9 . Найдите значение выражения:
a) -6·a²·b³=-3·(2·a²·b³)=-3·9= -27;
b) 2·a⁴·b⁶=(4·a⁴·b⁶):2=(2·a²·b³)²:2=(9)²:2=81:2= 40,5.