Определить,при каких значениях параметра а уравнение cos^2x+(2a+6)cosx+(2a-7)(1-4a)=0 имеет решения

👇

Ответ:

timon7901

29.03.2021

Методом замены переменной пусть t=cos x

Тогда наше уравнение будет иметь вид:
t^2+(2а+6)t+(2a-7)(1-4a)=0
У этого уравнения будут решения тогда, когда дискриминант будет положителен или равен 0
Из этого ограничения находим а

4,5(11 оценок)

Открыть все ответы

Ответ:

12345678300

29.03.2021

1. Итак, нам нужно понять какая эта функция! Для этого Вспомним, что функция f(x )-называется четной( нечетной), если для любого x∈D(f) и выполняется равенство f(x)=f(-x).

График четной функции симметричен относительно оси .

График нечетной функции симметричен относительно начала координат

Наш пример : y=x²-cos2x

Функция определенна при x∈(-∞;∞) , то есть f(-x)=(-x)²-cos2(-x)=-x²-cos2x=-(x²-cos2x)-функция является четной, т.к cosx-четная функция

2.Нам нужно сравнить два значения sin(-20°) V sin(-85)°, где V- знак сравнения ( птичкой называют)

Итак, sin(-20°)=sin(-10°)+sin30°≈0,1736+0,5≈-0,34

sin(-85°)=sin(-5°)-sin(90°)≈0,0872+1≈0,9999=грубо 1

sin(-20°) > sin(-85°). Есть еще более простой смотри поскольку числа не четные, пусть в место sin(-20°) будет sin(-30°)=-0,5 и sin(-85°) бусть будет sin(-90)=-1 и так -0,5>-1

ответ: 1) y=x²-cos2x- функция четная ; 2)sin(-20°) > sin(-85°)

Надеюсь, твой педагог не такая уш придирчивая. Удачи тебе!

4,8(43 оценок)

Ответ:

bonbino1

29.03.2021

1. ОТВЕТ: например, 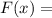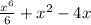F(x)= $\frac{x^6}{6}+x^2-4x$ , поскольку F'(x) = f(x) .

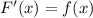Общий вид первообразных - 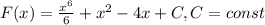$F(x)=\frac{x^6}{6}+x^2-4x+C, C=const$

2. Докажем, что 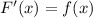F'(x)=f(x) :

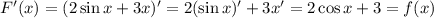$F'(x)=(2\sin x+3x)'=2(\sin x)'+3x'=2\cos x+3=f(x)$ .

Что и требовалось доказать.

3. Общий вид первообразных функции 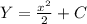y=x - $Y=\frac{x^2}{2}+C$ , где 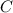- некоторое постоянное число. Если график первообразной проходит через точку 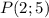P(2;5) , то это значит, что при подстановке 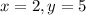x=2, y=5 получим верное равенство:

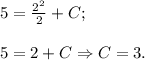
$5=\frac{2^2}{2}+C;\\\\5=2+C\Rightarrow C=3.$

Искомая первообразная - 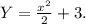$Y=\frac{x^2}{2}+3.$

ОТВЕТ: Y = x²/2 + 3.

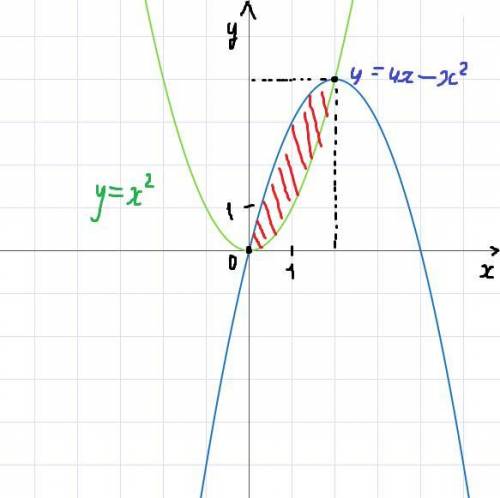
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.

Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид

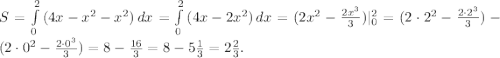
$S=\int\limits^2_0 {(4x-x^2-x^2)} \, dx =\int\limits^2_0 {(4x-2x^2)} \, dx =(2x^2-\frac{2x^3}{3})|^2_0=(2\cdot2^2-\frac{2\cdot2^3}{3})-(2\cdot0^2-\frac{2\cdot0^3}{3})=8-\frac{16}{3}=8-5\frac{1}{3}=2\frac{2}{3}.$

ОТВЕТ: 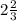$2\frac{2}{3}$ кв. ед.

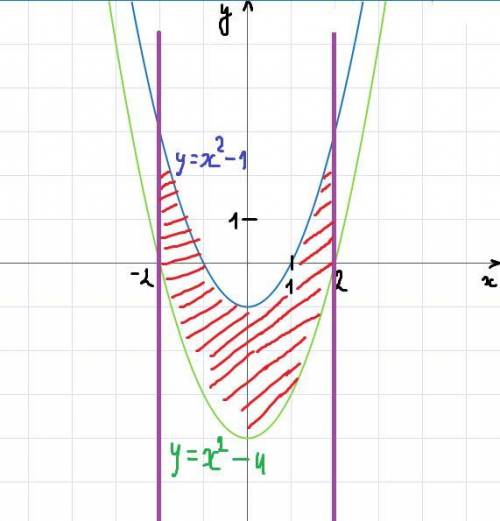
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.

Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид

$S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12$

ОТВЕТ: 12 кв. ед.

6. Объем выполненной работы A(t) с момента 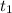t_1 по момент 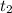t_2 согласно механическому смыслу определенного интеграла есть значение выражения интеграла

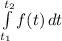
$\int\limits^{t_2}_{t_1} {f(t)} \, dt$

Имеем:

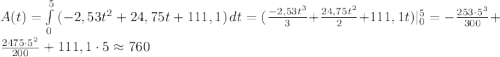
$A(t)=\int\limits^5_0 {(-2,53t^2+24,75t+111,1)} \, dt=(\frac{-2,53t^3}{3}+\frac{24,75t^2}{2}+111,1t)|_0^5=-\frac{253\cdot5^3}{300}+\frac{2475\cdot5^2}{200}+111,1\cdot5\approx760$