В решении.
Объяснение:
220.
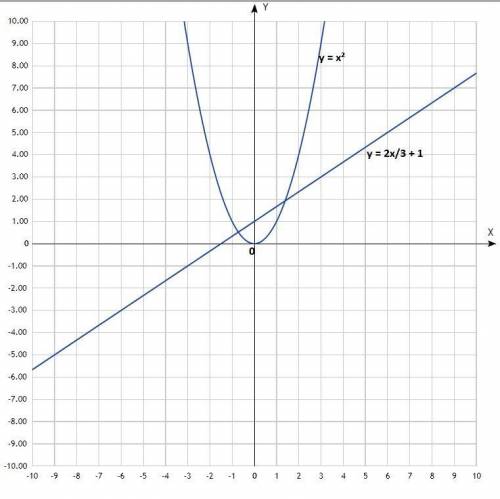
1) Построить графики: у = х²; 2х - 3у + 3 = 0.
Первый - классическая парабола, второй - прямая линия.
Преобразовать второе уравнение в уравнение функции:
2х - 3у + 3 = 0;
-3у = -2х - 3
3у = 2х + 3
у = (2х + 3)/3
у = 2х/3 + 1;
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 2х/3 + 1;
Таблицы:
х -3 -2 -1 0 1 2 3 х -3 0 3
у 9 4 1 0 1 4 9 у -1 1 3
По вычисленным точкам построить графики.
Согласно рисунка, координаты точек пересечения графиков:
(-0,7; 0,5); (1,4; 1,9).
2)
а) Решить графически систему уравнений:
у = х²
2х - 3у + 3 = 0
Графическое решение в 1).
Решения системы уравнений: (-0,7; 0,5); (1,4; 1,9).
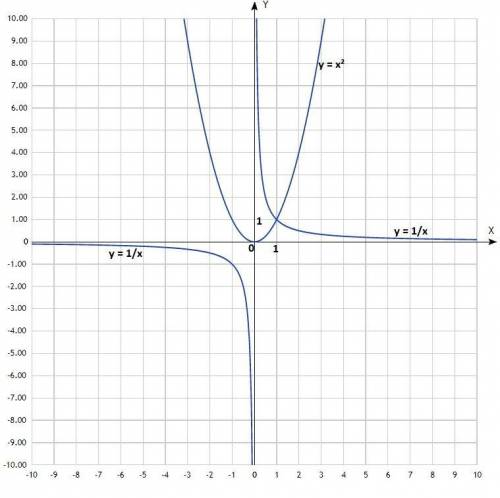
б) у = х²;
у = 1/х;
Построить графики. Первый - классическая парабола, второй - гипербола.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 1/х;
Таблицы:
х -3 -2 -1 0 1 2 3 х -10 -5 -2 -1 0 1 2 5 10
у 9 4 1 0 1 4 9 у -0,1 -0,2 -0,5 -1 - 1 0,5 0,2 0,1
По вычисленным точкам построить графики.
Согласно рисунка, координаты точки пересечения графиков: (1; 1).
Решение системы уравнений: (1; 1).
Задание 1:
Общий вид линейной функции: у = kx + b.
Число k является угловым коэффициентом. Если он отрицательный (меньше нуля), то функция убывает, а если положительный (больше нуля), то функция возрастает.
Взглянем на данную функцию:
y = 3x + 2
k = 3 > 0, поэтому функция возрастает.
Задание 2:
y = 2x + 3 — это линейная функция. Она достигает наибольшего и наименьшего значений на концах отрезка.
Вычислим их, подставив числа на концах промежутка [-1;3] в формулу:
у (-1) = 2 * (-1) + 3 = 1;
у (3) = 2 * 3 + 3 = 9.
Теперь выберем из полученных значений наименьшее и наибольшее.
Таким образом:
у наим. = 1;
у наиб. = 9.
a>0 → ветви параболы вверх. при а<0 были бы вниз.∨
x=0 → y=13
x^2 - 8x +13=0 D=b²-4ac=64-52=12 √D=2√3
x1=1/2[8+2√3]=4+√3 x2=4-√3 - точки пересения с осью х.
точка минимума x0=-b/2a=8/2=4 y0=16-32+13=-3
можно иначе y'=2x-8 2x-8=0 x=4 точка экстремума.
4→y'
- +
ф-я убывает от -∞ до 4 и возрастает при х от 4 до ∞, в точке
х=4 минимум.