
Объяснение:
Ищем точки пересечения с осью ОХ
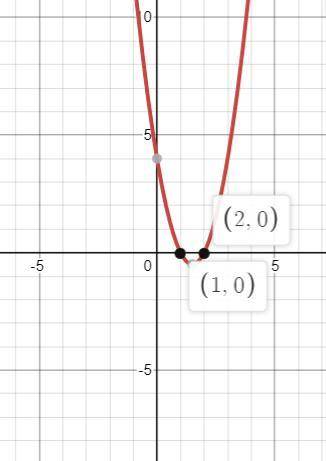
1) Ветви параболы направлены вверх, вершина x₀=-b/2а=6/4=1,5
точки пересечения с осью ОХ:
2x² - 6x + 4=0;
D=36-4*4*2=4; x₁=(6-2)/4;x₁=1;x₂=(6+2)/4;x₂=2
x∈(1;2)
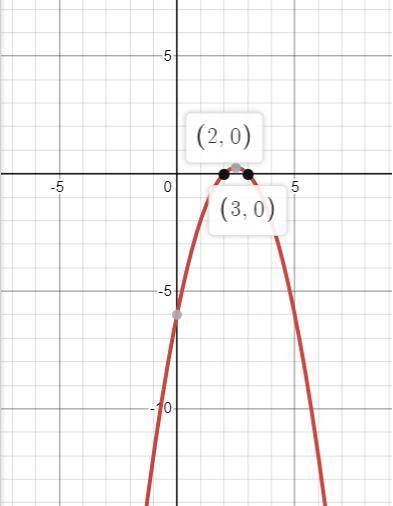
2) Ветви параболы направлены вниз ,вершина x₀=-b/2а=5/2=2,5
точки пересечения с осью ОХ:
x² -5x + 6=0; по т. Виета x₁=2; x₂=3
х∈(-∞;2)∪(3;∞)
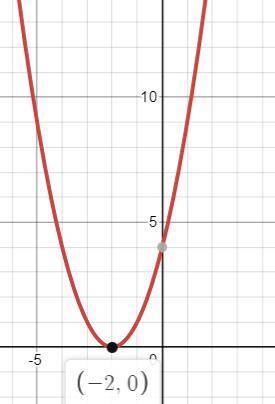
3)y = x² + 4x + 4; y=(х+2)²
y=(х+2)²=0; х=-2. Пересечение в одной точке и это же вершина
х∈∅
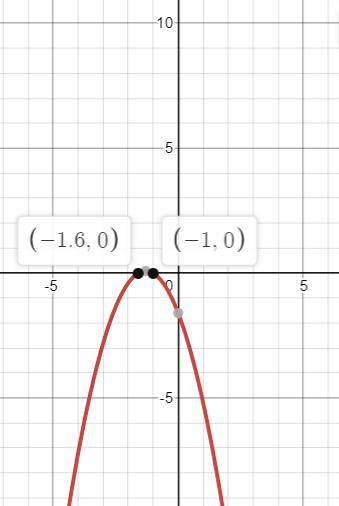
4) Ветви параболы вниз. Вершина x₀=-b/2а=2,6/2=1,3
точки пересечения с осью ОХ: x² + 2,6x + 1,6=0;
По т. Виета x₁=-1,6; x₂=-1.
х∈(-∞;-1,6)∪(-1;∞)
ответ:Пусть х-скорость катера в стоячей воде,
тогда скорость катера по течению равна х+2 км/ч,
а скорость катера против течения равна х-2 км/ч.
На путь по течению катер затратил 40/(х+2) часа,
а на путь против течения 6/(х-2) часа.
По условию на весь путь затрачено 3 часа.
Составим уравнение:
40/(х+2) + 6/(х-2) =3|*(x+2)(x-2)
40(x-2)+6(x+2)=3(x^2-4)
40x-80+6x+12=3x^2-12
46x-68-3x^2+12=0|*(-1)
3x^2-46x+56=0
D=2116-672=1444
x1=(46+38):6=14 (км/ч)
х2=(46-38):6=1 1/3 (км/ч) - проверкой устанавливаем, что этот корень не подходит 1 1/3-2<0
ответ: скорость катера в стоячей воде равна 14 км/ч
2. 130 - 20 = 110 м - две длины
3. 110 : 2 = 55 м - длина участка
4. 55 х 10 = 550 м^2