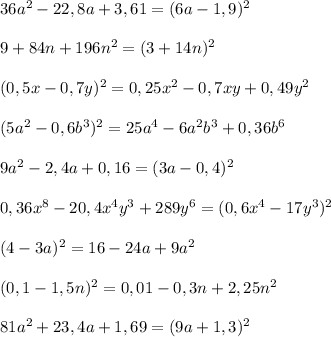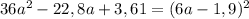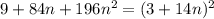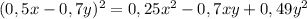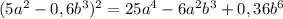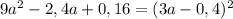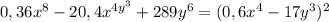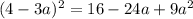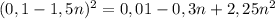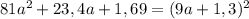Question

Представьте многочлен в виде квадрата суммы или разности: 36a^2−22,8a+3,61 представьте многочлен в виде квадрата двучлена: 9+84n+196n^2 представьте в виде многочлена выражение: (0,5x−0,7y)^2 выполните возведение в квадрат: (5a^2−0,6b^3)^2 представьте многочлен в виде квадрата суммы или разности: 9a^2−2,4a+0,16 представьте многочлен в виде квадрата суммы или разности: 0,36x^8−20,4x^4y^3+289y^6 выполните возведение в квадрат: (4−3a)^2 выражение (0,1−1,5n)^2 представьте многочлен в виде квадрата двучлена: 81a^2+23,4a+1,69

Answer 1

$36a^2-22,8a+3,61=(6a-1,9)^2\\\\9+84n+196n^2=(3+14n)^2\\\\(0,5x-0,7y)^2=0,25x^2-0,7xy+0,49y^2\\\\(5a^2-0,6b^3)^2=25a^4-6a^2b^3+0,36b^6\\\\9a^2-2,4a+0,16=(3a-0,4)^2\\\\0,36x^8-20,4x^4y^3+289y^6=(0,6x^4-17y^3)^2\\\\(4-3a)^2=16-24a+9a^2\\\\(0,1-1,5n)^2=0,01-0,3n+2,25n^2\\\\81a^2+23,4a+1,69=(9a+1,3)^2$

Answer 2

1) $36a ^{2} - 22,8a + 3,61 = (6a - 1,9) ^{2}$
2) $9 + 84n + 196n ^{2} = (3 + 14n) ^{2}$
3) $(0,5x - 0,7y) ^{2} = 0,25 x^{2} - 0,7xy + 0,49y ^{2}$
4)$(5a ^{2} - 0,6b ^{3} ) ^{2} = 25a ^{4} - 6a ^{2} b ^{3} + 0,36b ^{6}$
5) $9a ^{2} - 2,4a + 0,16 = (3a - 0,4) ^{2}$
6)$0,36x ^{8} - 20,4x ^{4y ^{3} } + 289y ^{6} = (0,6x ^{4} - 17y ^{3} ) ^{2}$
7) $(4 - 3a) ^{2} = 16 - 24a + 9a ^{2}$
8) $(0,1 - 1,5n) ^{2} = 0,01 - 0,3n + 2,25n ^{2}$
9) $81a ^{2} + 23,4a + 1,69 = (9a + 1,3) ^{2}$