* * * * * * * * * * * * * * * * * * * * * * * * *
Решите систему уравнений { 3xy -x =5 ; 3xy -y= 4
ответ: (x₁ ; y₁) = ( -5/3 ; -2/3 ) ; ( x₂ ; y₂) = (1 ; 2) .
Объяснение:
{ 3xy -x =5 ; 3xy -y= 4 . ⇔ { 3xy -x-(3xy -y) = 5 - 4 ; 3xy -x =5 . ⇔
{ y=x+1 ; 3xy - x =5 .⇔ { y=x+1 ; 3x(x+1) - x -5 =0 .⇔ { y=x+1 ; 3x²+2x -5 =0 .
3x²+2x -5 =0
D₁= D/4 =( 2/2)² - 3*(-5) =1²+15 =16 = 4² ; x = (-1 ± √D₁)/3
⇒ x₁ = (-1 -4) /3 = - 5/3 ⇒ y₁ = x₁+1 = -5/3+1 = -2/3
x₂ = (-1 +4) /3 = 1 ⇒ y₂ = x₂+1 =1 +1 = 2 .
ответ: 44
Объяснение:
Пусть х — количество учеников, которые были в комнатах по 4 человека. Тогда х/4 — количество четырёхместных комнат (х учеников расселили в комнаты по 4 человека). Количество человек, живших в трёхместных комнатах — 71-х (т. к. все, кто не жил в четырёхместных комнатах, жили в трёхместных). Тогда количество трёхместных комнат — (71-х)/3 (71-х человек расселили в комнаты по трое). Так как всего комнат 20, и они были только трёхместные и четырёхместные, получаем:
20=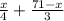 
(20 комнат — это все комнаты, и трёхместные, и четырёхместные).
Решим получившееся уравнение:
20=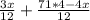
20 =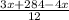 
20=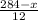 
Умножим обе части на 12:
240 = 284 - х
х = 284 - 240
х = 44
ответ: 44.
Примечание: чтобы убедиться в правильности ответа, можно сделать проверку:
Если в комнатах по 4 человека жили 44 ученика, всего четырёхместных комнат было 44/4=11.
Т. к. всего комнат 20, то трёхместрых комнат 20-11=9 комнат. Т. к. все они заполнены, в них должно жить 9*3=27 учеников.
После того, как 44 ученика поселили в четырёхместные комнаты, осталось 71-44=27 детей — именно столько должно было жить в трёхместных комнатах.
Проверка показала, что найденный ответ верен.
ответ: наибольшее значение выражения -x²-4 равно -4; достигается оно при x=0