![x^3+3x+2\sqrt[3]{x-4} -34=0](/tpl/images/1360/1028/6c477.png)
Запишем уравнение в виде:
![x^3+3x -34=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/bd4bd.png)
Пусть левая и правая часть равны у. Тогда получим систему:
![\begin{cases} y=x^3+3x -34\\y=-2\sqrt[3]{x-4}\end{cases}](/tpl/images/1360/1028/c1e6e.png)
Рассмотрим каждое уравнение как функцию.
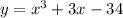- возрастающая функция, так как это кубическая парабола с положительным старшим коэффициентом
![y=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/0df79.png)
- убывающая функция, так как корень нечетной степени имеет сомножителем отрицательное число
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{0}](/tpl/images/1360/1028/d91f8.png)
, то есть 
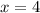. Проверим, является ли это число корнем:
![4^3+3\cdot4+2\sqrt[3]{4-4} -34=64+12+2\cdot0-34=42\neq 0](/tpl/images/1360/1028/6e40b.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{1}](/tpl/images/1360/1028/7bd4a.png)
, то есть 
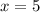. Проверим, является ли это число корнем:
![5^3+3\cdot5+2\sqrt[3]{5-4} -34=125+15+2\cdot1-34=108\neq 0](/tpl/images/1360/1028/f1f89.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{-1}](/tpl/images/1360/1028/4572f.png)
, то есть 
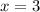. Проверим, является ли это число корнем:
![3^3+3\cdot3+2\sqrt[3]{3-4} -34=27+9+2\cdot(-1)-34=0](/tpl/images/1360/1028/fd423.png)
- корень
Таким образом, уравнение имеет единственный корень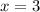
ответ: 3
Суть в том, что четырехугольник надо разбить на два треугольника, проведя СK. Тогда площадь треугольника МКС будет равна площади треугольника АКМ (так как проведена медиана). Если обозначить площадь треугольника АВК за S, то площадь АКМ=площадьМКС=1,5 S. Если обозначить площадь треугольника КВР за S1, то площадь треугольника КРС будет равна 3S1 (треугольники подобны). Так как площадь треугольников АВМ и МВС равны (проведена медиана), и площади АКМ и КМС равны, значит, площади АВК и ВКС тоже равны. Получается, что S=S1+3S1 => S=4S1. Далее, отношение площади АВК к КРСМ будет равно отношению S к (3S1+1,5S), куда вместо S1 нужно подставить 0,25S, в итоге получается 4/9.
ответ: 4/9
4-x² ≥0
х² ≤ 4
-2≤ х ≤2 х∈ [-2 ;2]