Парабола: y = ах^2 + bx + c
1)
A: 16a - 4b + c = 0
B: 4a + 2b + c = 0
C: 0a + 0b + c = -3
<=>
c = -3
16a - 4b = 3
4a + 2b = 3 (* 2) и сложим
<=>
c = -3
4a - 2b = 3
24a = 9
<=>
c = -3
a = 3/8
b = 2a - 3/2 = -3/4
=> Уравнение: y = 3/8 x^2 - 3/4 x - 3
2) (Другой
Используем Th Виета
x1 + x2 = -b/a
x1 * x2 = c/a
что означает, что a x^2 + bx + c = 0 ?
это значит, что х - корень
т.к. в Точках A и B y = 0 => корни: 1 и 6
=> 7 = -b/a
6 = c/a
Посмотрим на 3-ю точку
a * 0 + b * 0 + c= -4
=> c = -4
=> 7 = -b / a
6 = -4/a
=> a = -2/3
b = 21/2
=> Уравнение: y = -2/3x^2 + 21/2x - 4
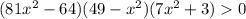
7x² + 3 > 0 при любых значениях x , разделим обе части неравенства на это положительное число и знак неравенства при этом не изменится.
Получим :
(81x² - 64)(49 - x²) > 0
(81x² - 64)(x² - 49) < 0
(9x - 8)(9x + 8)(x - 7)(x + 7) < 0

+ - + - +
_______₀_________₀__________₀_______₀__________
- 7 - 8/9 8/9 7
x ∈ (- 7 ; - 8/9) ∪ (8/9 ; 7)
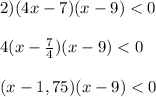
+ - +
__________₀___________₀___________
1,75 9
x ∈ (1,75 ; 9)