![\begin{array}{lll} y=-x^{3}+3x^{2}+4.\mapsto \in \text{[-3;3]}& y=ln(4x)-4x+5.\mapsto [\frac{1}{8} ;\frac{5}{8} ]& y=32tg(x)-32x-8\pi +7.\mapsto \text{[}-\frac{\pi }{4} ;\frac{\pi }{4} ]\\ & & \frac{d}{dx} (32tg(x)-32x-8\pi +7)=32sec^{2}(x)-32=0\\ & \frac{d}{dx} (ln(4x)-4x+5)=\frac{1-4x}{x} =0& sec(x)=\pm 1\mapsto x=k\pi ,k\in \mathbb{Z} \text{k\pi }\notin [-\frac{\pi }{4} ;\frac{\pi }{4} ]\\ \frac{d}{dx} (-x^{3}+3x^{2}+4)=-3x^{2}+6x=-3x(x-2)=0& x=\frac{1}{4} \mapsto \in [\frac{1}{8} ;\frac{5}{8} ]& x=-\frac{\pi }{4} \\ & & y=-32+8\pi -8\pi +7=-25.\\ x_{1}=0\mapsto \in \text{[-3;3]};\text{x}_{2}=2.\mapsto \in \text{[-3;3]}& y=ln(\frac{1}{2} )-\frac{1}{2} +5=-ln(2)+\frac{9}{2} \approx 3.80685& x=\frac{\pi }{4} \\ y=27+27+4=58.& y=ln(1)-1+5=4.& y=32-8\pi -8\pi +7=39-16\pi \approx -11.26548.\\ x=0& x=\frac{5}{8} & \text{Max=-11.26548};\text{Min=-25}.\\ y=0+0+4=4.& y=ln(\frac{5}{2} )-\frac{5}{2} +5\approx 3.41629& \\ x=2& Max=4;\text{Min\approx 3.41629}& \\ y=-8+12+4=8.& & \\ x=3.& & \\ y=-27+27+4=4.& & \\ Max=58;\text{Min=4}& & \end{array}](/tpl/images/0827/8723/4518a.png)
Объяснение:5)5-2ax=14+2x; 6)3(8-3ах)=8-ах;
-2ax-2x=14-5; 24-9ах=8-ах;
-2x(a+1)=9; -9ах+ах=8-24;
x= - 9/2(a+1). 8ах=16
ур-ие имеет решение при ∀ а≠-1. ах=2 -
а≠0.
7)7х(а-8)=-5 -ур-ие имеет решение
при всех значениях а≠8.
8)3х(а+7)=7
ур-ие имеет решение при всех значениях а≠ -7.
1)
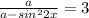
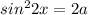
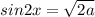
Так как значения синуса не могут быть большими единицы, получаем:
Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:
Откуда получаем:
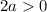
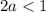
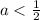
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)
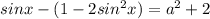
Получаем квадратное уравнение относительно t:
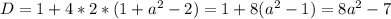
Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
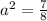
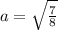
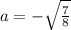
Но так как нам нужно только одно решение в заданном промежутке получаем:
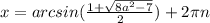
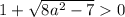
неравенство не имеет решений
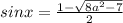
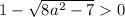
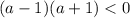
Получаем, что при a∈
данное уравнение имеет лишь один корень
ответ: a∈
