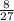 + log₃18 можно также упростить с помощью свойств логарифмов. Здесь мы воспользуемся свойством, которое гласит, что разность логарифмов с одинаковым основанием эквивалентна взятию логарифма от частного. То есть, log₃36 - log₃
+ log₃18 можно также упростить с помощью свойств логарифмов. Здесь мы воспользуемся свойством, которое гласит, что разность логарифмов с одинаковым основанием эквивалентна взятию логарифма от частного. То есть, log₃36 - log₃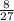 + log₃18 = log₃(36/(
+ log₃18 = log₃(36/(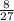 *18)).
*18)).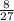 *18), мы можем сократить числитель и знаменатель на их общий делитель. Общий делитель в данном случае это 18, поэтому дробь станет равна 2/8 = 1/4.
*18), мы можем сократить числитель и знаменатель на их общий делитель. Общий делитель в данном случае это 18, поэтому дробь станет равна 2/8 = 1/4. *18)) = log₃(1/4). Логарифм от 1/4 по основанию 3 можно записать как -log₃4. Таким образом, выражение становится равным log₃4.
*18)) = log₃(1/4). Логарифм от 1/4 по основанию 3 можно записать как -log₃4. Таким образом, выражение становится равным log₃4.
а) 5х+3=х-5. х1=-1/2. х2=нет.
б) х²+1=5. х1=-2. х2=2.
д) (х-31)(х+2)=0. х1=31. х2=-2.
е) -х=4,5-2,5. х1=-2. х2=нет.
в) -3х+4=12-х. х1=-4. х2=нет.
г) |х|=2х+6. х1=-6. х2=-2.
б;д;г
2. (4-х)(х+10)(х-3)=0. х1=4. х2=-10. х3=3.
(4-4)(4+10)(4-3)=0•14•1=0.
3. а) |х|=2. х=±2. б) |х|=0. х=0.
±0 невозможно
в) |х|=-77. х=±77. 3. б